Golden Ratio in Math and Nature – Complete Guide with Visuals
If you've ever wondered what the golden ratio is in math, you're not alone. Students often encounter this mysterious number—approximately 1.618—and struggle to understand what makes it so special. The golden ratio appears in mathematical formulas, natural patterns like sunflower spirals and seashells, and even in art and architecture throughout history.
This complete guide will explain the concept simply, show you visual examples, walk through the formula step-by-step, and connect mathematical theory to real-world patterns you can recognize. Whether you're studying geometry, exploring nature, or curious about design principles, understanding the golden ratio (φ) will help you see the mathematical beauty in the world around you. Let's explore the diagrams, examples, and practical applications together.
What Is the Golden Ratio in Math?
The golden ratio in math is a special number—approximately φ ≈ 1.6180339887 — that appears when the ratio of two quantities equals the ratio of their sum to the larger quantity. This unique proportion creates naturally balanced and visually pleasing relationships between numbers.
Here's how it works: when you have two numbers, a and b (where a is larger), the golden ratio occurs when:
φ = (1 + √5) / 2
Or expressed as a proportion:
a/b = (a + b)/a = φ
This means dividing the larger number by the smaller gives you approximately 1.618, and dividing the sum of both by the larger also gives you 1.618.
You might also see it spelled as "what is the golden ratio in maths" in some regions—both refer to the same mathematical constant represented by the Greek letter phi (φ).
Why is the golden ratio important?
Used in geometry to create golden rectangles and pentagons
Appears in natural patterns like spirals and growth sequences
Applied in design and art for balanced compositions
Creates visually pleasing proportions that feel harmonious
Connects to the Fibonacci sequence through ratio patterns
Golden Ratio Formula Explained Step-by-Step
Let's break down the golden ratio formula with a simple example:
Formula: φ = (1 + √5) / 2
Step-by-step calculation:
Calculate the square root of 5: √5 ≈ 2.236
Add 1: 1 + 2.236 = 3.236
Divide by 2: 3.236 ÷ 2 ≈ 1.618
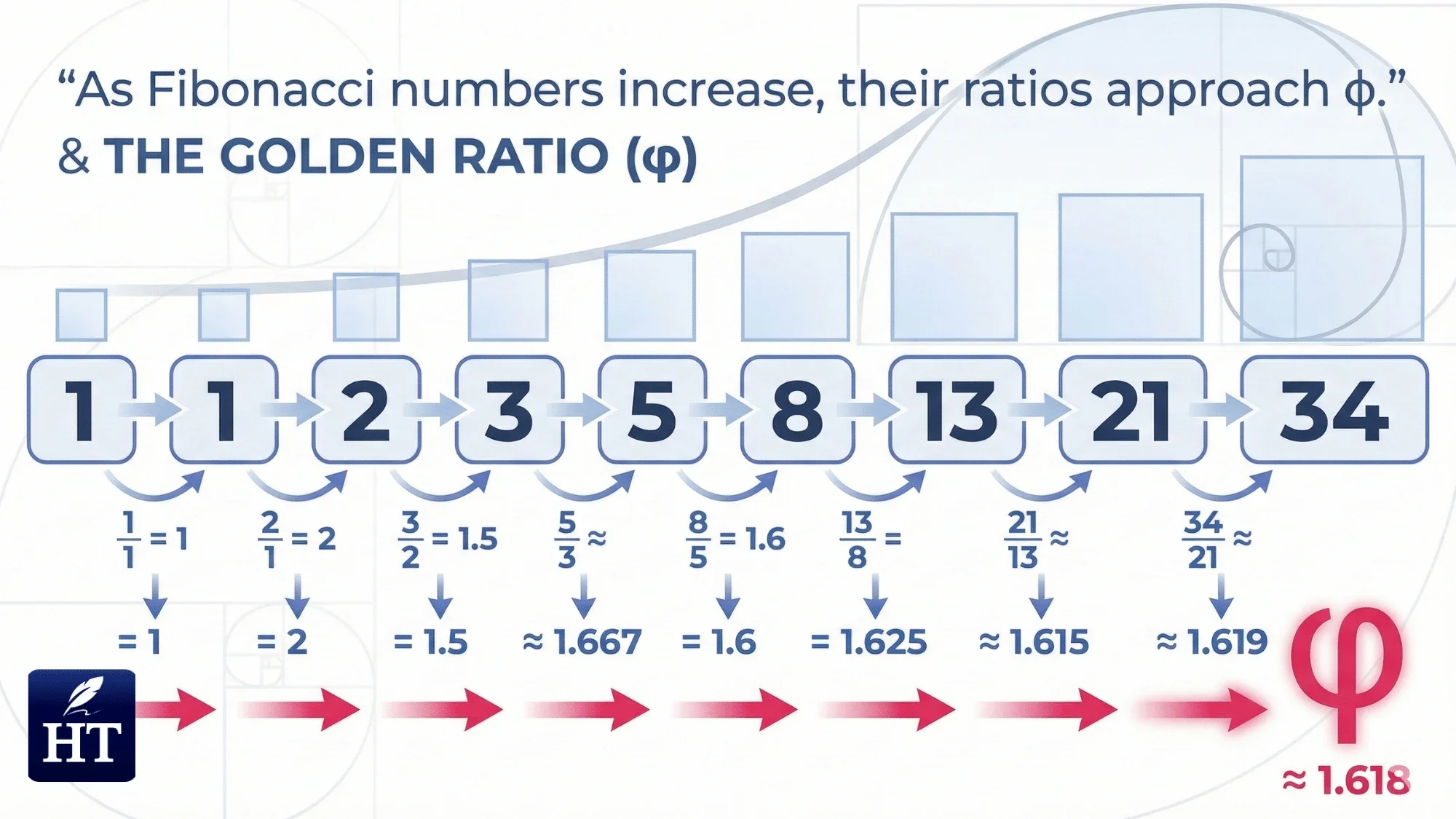
Real example using consecutive Fibonacci numbers:
Take 34 and 21
Divide: 34 ÷ 21 ≈ 1.619
This approximates φ (the larger the Fibonacci numbers, the closer they get to exactly 1.618)
No complex derivations needed—just remember that phi is approximately 1.618, and you can test any two numbers to see if they're in the golden ratio.
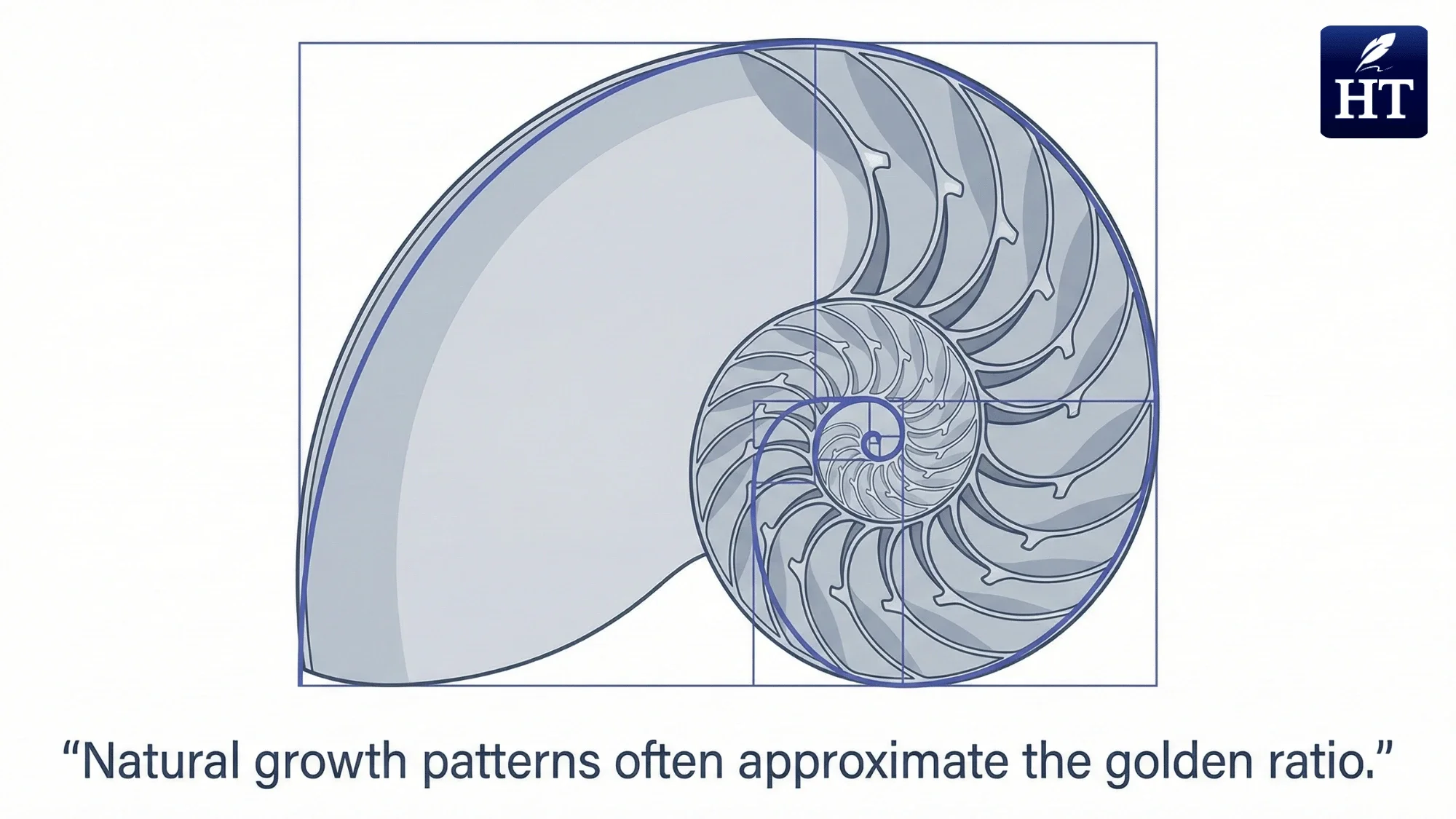
Golden Ratio in Nature (With Visual Examples)
The golden ratio in nature appears in surprising places, from tiny shells to vast spiral galaxies. While nature doesn't follow mathematical formulas perfectly, many natural growth patterns approximate the golden ratio remarkably closely.
Where you'll find golden ratio patterns in nature:
Sunflower seed heads – Spirals of seeds often follow Fibonacci patterns that approximate φ
Nautilus shells – The spiral chambers grow in proportions close to the golden ratio
Pinecones and pineapples – Spiral patterns in overlapping scales frequently show golden ratio relationships
Flower petals – Many flowers have petal counts that are Fibonacci numbers (3, 5, 8, 13, 21)
Tree branches – The way branches split and grow often resembles golden ratio proportions
Hurricane formations – Large-scale spirals in weather systems approximate logarithmic spirals related to φ
These patterns emerge because the golden ratio represents an efficient packing and growth strategy. When plants arrange seeds or petals using these proportions, they maximize space and access to sunlight.
Golden Ratio in Art, Architecture & Design
Artists and architects have used the golden ratio formula for centuries to create balanced, aesthetically pleasing compositions. While some historical claims are exaggerated, credible examples demonstrate how φ creates visual harmony.
Examples of the golden ratio in human creations:
The Parthenon – Greek architects used proportions close to the golden ratio in the facade dimensions
Renaissance paintings – Artists like Leonardo da Vinci applied golden rectangles to position focal points in compositions
Modern logo design – Companies like Apple and Twitter have incorporated golden ratio spirals in their branding (though not all claims are verified)
Architecture – Le Corbusier's Modulor system explicitly used phi to determine human-scale proportions in buildings
Photography composition – The "rule of thirds" relates to golden ratio divisions for placing subjects
Designers favor these proportions because they create visual balance without perfect symmetry—making compositions feel natural and dynamic rather than static.
How to Calculate the Golden Ratio (Easy Steps)
Want to check if two numbers follow the golden ratio in math? Here's a simple method:
Divide the larger number by the smaller number – For example: 89 ÷ 55 = 1.618
Check if the result is close to 1.618 – If it's approximately 1.618 (or between 1.61 and 1.62), you've found the golden ratio
Alternative: Use the formula directly – Calculate (1 + √5) / 2 to get the exact value
Numerical Example:
Take two measurements: 8 inches and 5 inches
Divide: 8 ÷ 5 = 1.6
This is close to φ, making it an approximate golden ratio
Teacher Tip: The easiest way to create golden ratio proportions is to start with any Fibonacci number and divide it by the previous Fibonacci number. The further you go in the sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...), the closer you get to exactly 1.618.
Real-Life Examples Students Can Recognize
Understanding what is the golden ratio in maths becomes easier when you see it in everyday objects:
Credit cards and ID cards – The length-to-width ratio approximates the golden rectangle (about 1.6:1)
Paper sizes – Some international paper formats use proportions close to φ
Smartphone screens – Many modern devices use aspect ratios near the golden ratio for visual appeal
Website layouts – Designers use golden ratio grids to position sidebars and content areas
Photography framing – Professional photographers place horizons and subjects at golden ratio divisions
Book page layouts – Margins and text blocks often follow golden rectangle proportions
Nature observation – Count the spirals on a pineapple or pinecone—they're usually Fibonacci numbers
These practical examples help students see how mathematical concepts connect to the designed and natural world around them.
Conclusion
The golden ratio in math is far more than just the number 1.618—it's a fundamental proportion that bridges mathematics, nature, art, and design. By understanding how φ emerges from the formula (1 + √5) / 2 and recognizing its connection to the Fibonacci sequence, students gain insight into one of mathematics' most elegant patterns.
Whether you're analyzing geometric shapes, observing spiral patterns in nature, or learning design principles, the golden ratio helps you appreciate the mathematical harmony underlying visual beauty. Understanding this concept strengthens your foundation in geometry while revealing how mathematical thinking applies to real-world patterns and creative work.
Ready to explore more essential math concepts? Visit HYE Tutors for comprehensive guides on algebra, geometry, and mathematical reasoning designed specifically for students building their skills.