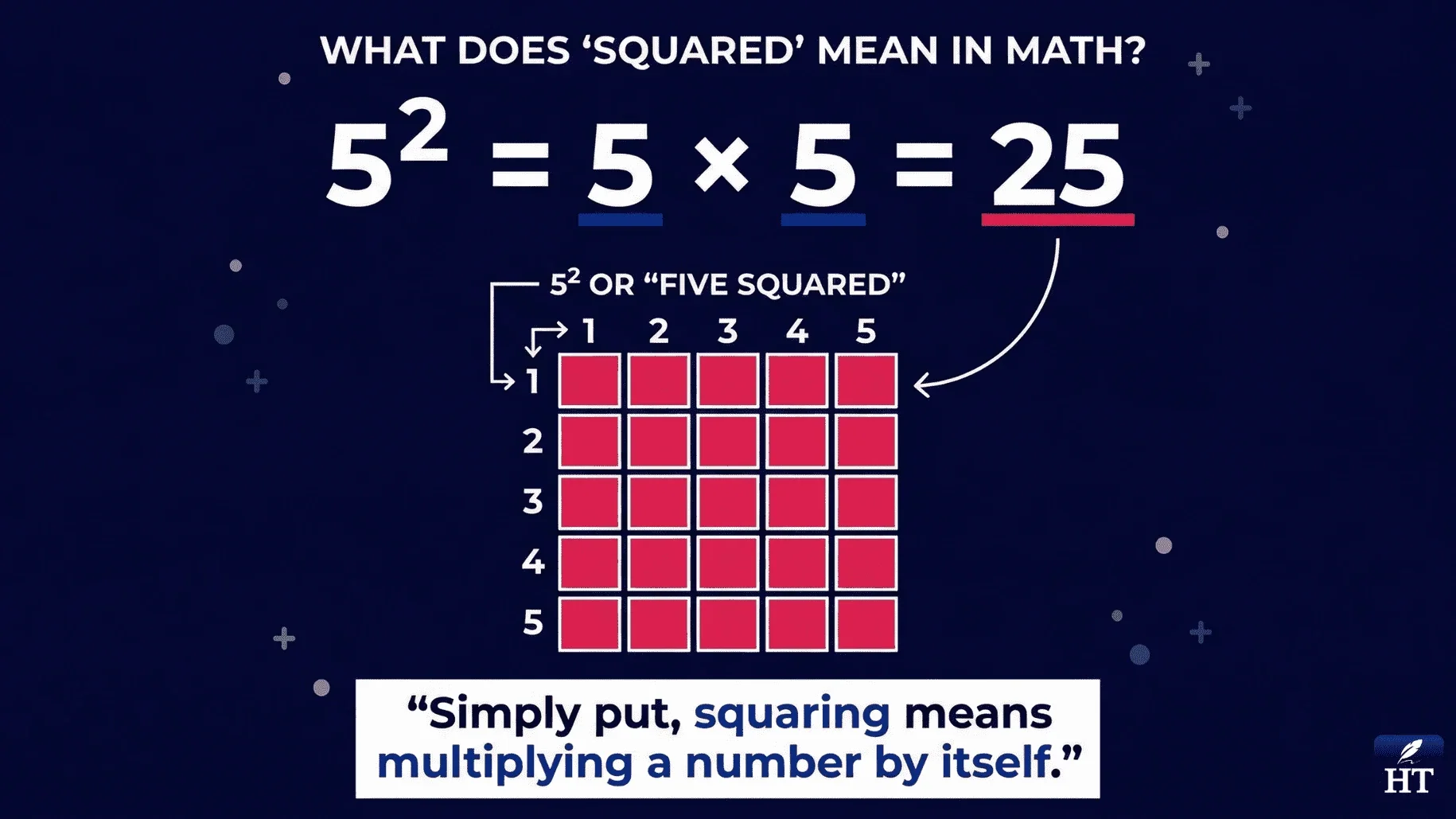‘Squared’ in Math Explained

If you've ever wondered what does squared mean in math, you're asking one of the most fundamental questions in algebra and geometry. Students frequently encounter the small "²" symbol in formulas and equations but struggle to understand what it represents, how to calculate it, and why it appears so often in mathematical problems. Simply put, squaring means multiplying a number by itself, but there's much more to this concept than just multiplication.

This comprehensive guide will explain what squared means, show you how to recognize and use the exponent 2 symbol, demonstrate real-life applications, and clarify how squaring differs from related concepts like square roots and square brackets. You'll see clear examples, step-by-step calculations, and visual comparisons designed to build your confidence with squared numbers. Let's explore this essential math concept together.

“Squared in math means multiplying a number by itself. It is written with the exponent 2, like 5², which equals 5 × 5 = 25. Squaring is used in geometry, formulas, and real-life measurements such as area. If a number has a superscript 2, it means the number is being squared.”

— HYS Tutors

What Does Squared Mean in Math?

Squared in math means multiplying a number by itself. When you see a number with the exponent 2 (written as a small superscript), it tells you to multiply that number by itself once. For example, 5² means 5 × 5, which equals 25.

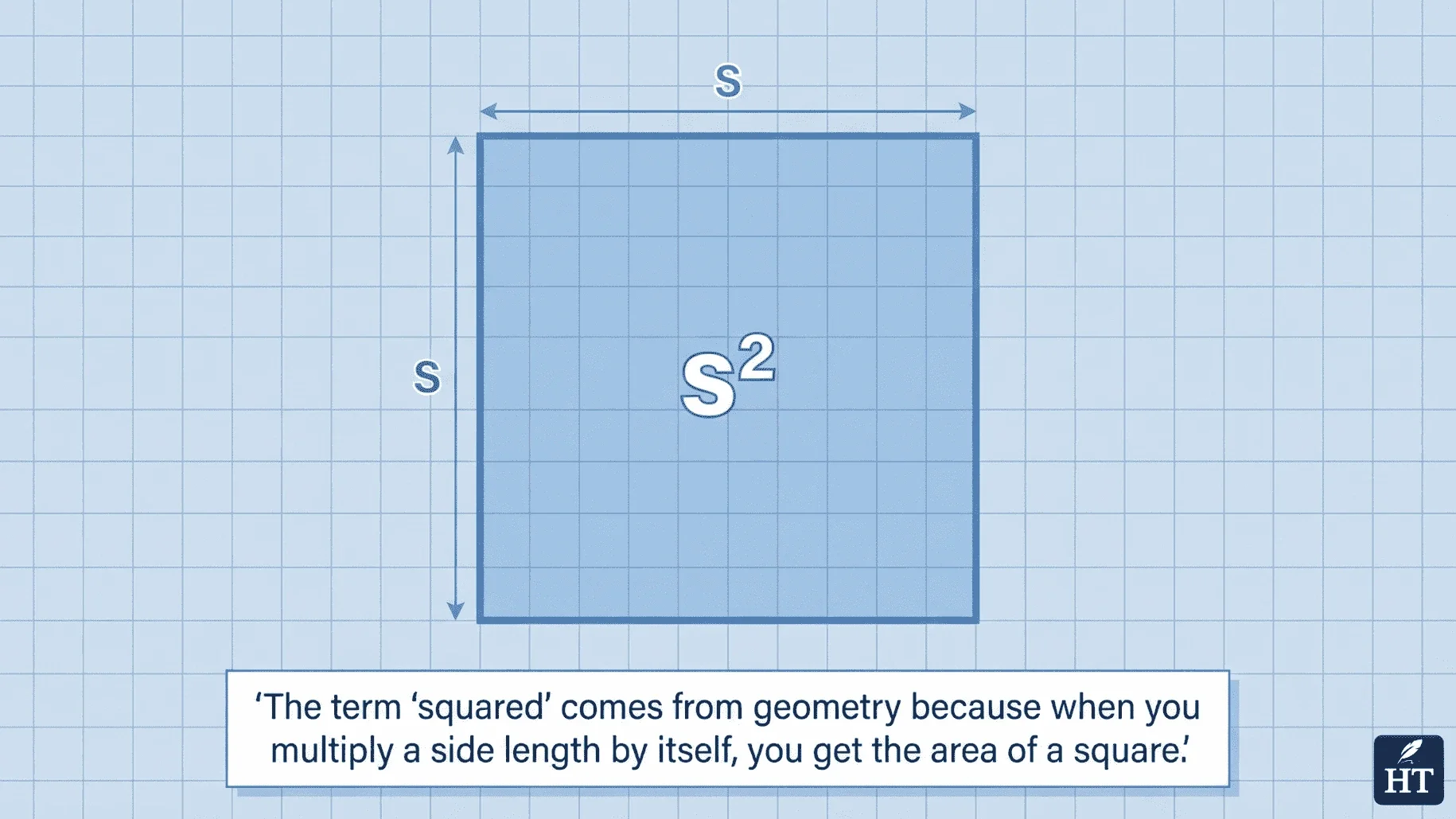
You might also see this concept described as "what does square mean in math" or "in math what does squared mean"—all refer to the same operation of taking a number to the second power. The term "squared" comes from geometry because when you multiply a side length by itself, you get the area of a square.

Simple numeric examples:

• 3² = 3 × 3 = 9

• 7² = 7 × 7 = 49

• 10² = 10 × 10 = 100

• 12² = 12 × 12 = 144

The notation uses a superscript 2 positioned above and to the right of the base number. This math exponent tells you how many times to use the number in multiplication with itself.

Squared numbers appear constantly in mathematics because they're essential for calculating areas, working with the Pythagorean theorem, understanding quadratic equations, and analyzing exponential growth patterns.

How Squaring Works (With Simple Examples)

Understanding how to square a number is straightforward with these step-by-step examples:

• 4² calculation: Write 4 × 4, then multiply to get 16

• 6² calculation: Write 6 × 6, then multiply to get 36

• 8² calculation: Write 8 × 8, then multiply to get 64

• 15² calculation: Write 15 × 15, then multiply to get 225

• 20² calculation: Write 20 × 20, then multiply to get 400

• Pattern observation: Notice that squared numbers grow quickly—doubling a number more than doubles its square

Why Squared Numbers Matter in Math

Squared numbers are fundamental to many mathematical concepts and real-world applications:

• Geometry and measurement – Calculating the area of squares and circles (πr²)

• Algebra – Solving quadratic equations and working with polynomials

• Physics formulas – Kinetic energy (½mv²), gravitational force calculations, and acceleration

• Statistics and data analysis – Variance calculations and error measurements use squared values

• Pythagorean theorem – Finding distances using a² + b² = c²

• Number theory – Understanding perfect squares and numerical patterns

Symbol and Notation for Squared Numbers

The "²" exponent symbol is the standard way to show that a number is being squared. This small superscript number indicates the operation of multiplying the base number by itself.

How squaring appears in different contexts:

• Written mathematics: 9² (read as "nine squared")

• Calculator notation: 9^2 or 9** (depending on calculator type)

• Digital typing: Use the caret symbol: 9^2 when superscripts aren't available

• Computer programming: Math.pow(9, 2) or 9**2 in various programming languages

• Spreadsheet formulas: =9^2 or =POWER(9,2)

When you see what does squared mean in math problems, the ² symbol always means the same operation: multiply the base by itself exactly once.

Examples you can copy:

• Area formula: A = s² (where s is the side length)

• Distance formula: d² = x² + y²

• Quadratic term: ax² + bx + c

Common Mistakes Students Make

Avoid these frequent errors when working with squared numbers:

• Missing parentheses: Writing -5² when you mean (-5)² leads to incorrect answers (the first equals -25, the second equals +25)

• Confusing x² with 2x: These are completely different—5² = 25 but 2(5) = 10

• Squaring only part of an expression: (3 + 4)² ≠ 3² + 4²—you must add first, then square

• Forgetting the exponent: Writing 5 × 5 as just 5 instead of 5²

• Mixing up order of operations: Remember that exponents come before multiplication and division

Real-Life Examples of Squared Numbers

Understanding what does square mean in math becomes clearer when you see practical applications in everyday situations:

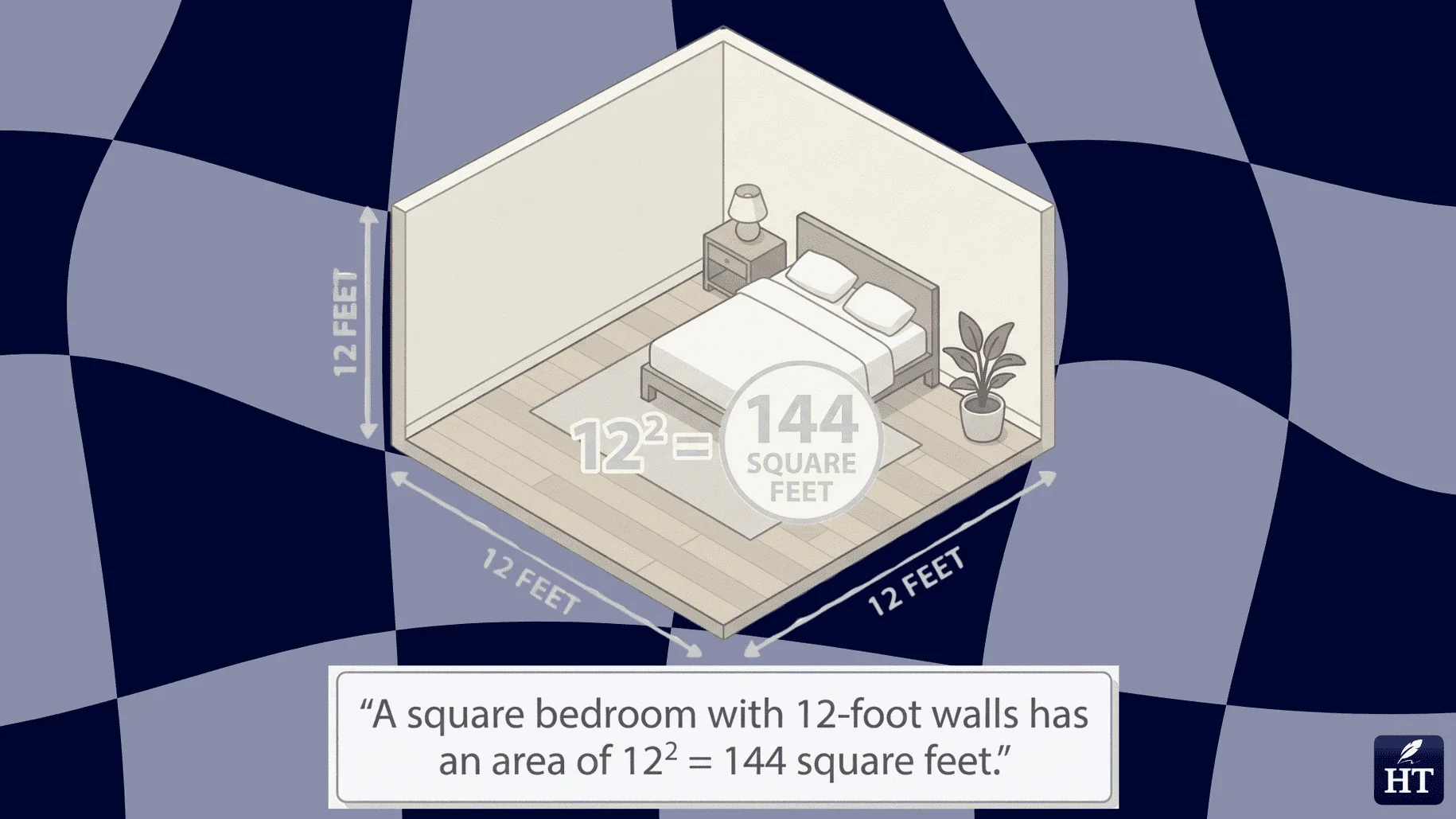
Room area calculations

• A square bedroom with 12-foot walls has an area of 12² = 144 square feet

• Flooring, carpet, and paint coverage all require squared measurements

Physics and motion

• The distance formula for falling objects uses time squared: d = ½gt²

• Kinetic energy depends on velocity squared: KE = ½mv²

• This explains why doubling your speed requires four times the stopping distance

Map scaling and proportions

• If a map scale is 1:100, areas are scaled by 100² = 10,000

• Doubling dimensions makes areas four times larger, not twice as large

Technology and displays

• Screen resolution is measured in pixels—a 1080p screen has 1920 × 1080 pixels

• Increasing pixel density improves image quality using squared relationships

Financial growth patterns

• Compound interest calculations use squared terms for multi-year growth

• Understanding how values grow exponentially requires working with exponents

Construction and engineering

• Calculating materials for square foundations, tiles, or panels

• Structural strength often depends on dimension-squared relationships

These examples show how squaring appears in measurements, science, technology, and daily planning.

Square vs Square Root (Clear Difference)

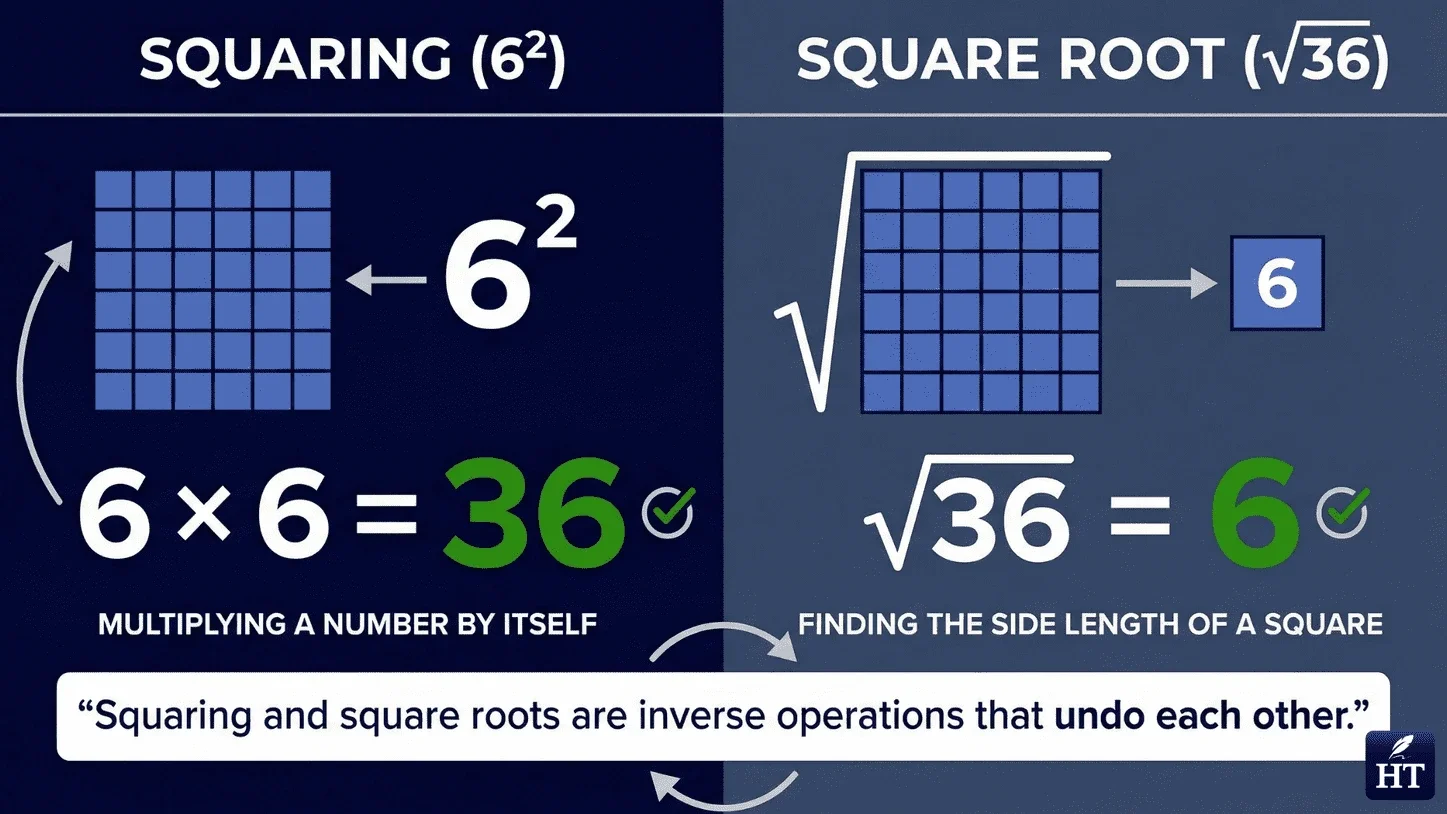
Many students confuse squaring with finding a square root—these are actually inverse operations that undo each other. A square root asks "what number, when multiplied by itself, gives this result?"

The fundamental relationship:

• Squaring takes a number to its square: 5² = 25

• Square root returns to the original: √25 = 5

Operation	Symbol	Example	Result	Meaning
Square	²	6²	36	Multiply 6 by itself
Square Root	√	√36	6	Find what number squared equals 36
Square	²	10²	100	Multiply 10 by itself
Square Root	√	√100	10	Find what number squared equals 100

Think of square and square root as opposites—they reverse each other's effects, similar to how addition and subtraction work together.

When searching "what does square root mean in math," remember: it's the operation that finds the original number before squaring.

Examples of Square and Square Root Pairs

These pairs demonstrate the inverse relationship:

• 25 ↔ 5: Because 5² = 25, we know √25 = 5

• 100 ↔ 10: Because 10² = 100, we know √100 = 10

• 144 ↔ 12: Because 12² = 144, we know √144 = 12

• 64 ↔ 8: Because 8² = 64, we know √64 = 8

• 196 ↔ 14: Because 14² = 196, we know √196 = 14

Understanding this connection helps you check your work—if you square a number and then take the square root, you return to where you started.

How to Square Any Number (Step-by-Step Guide)

Learning to square a number efficiently improves your mathematical confidence. Here are practical methods for different situations:

Method 1: Direct multiplication

1. Write the number twice with a multiplication sign between

2. Multiply using your preferred technique

3. Example: 13² → 13 × 13 = 169

Method 2: Using a calculator

1. Enter the number

2. Press the x² button (or use ^ 2)

3. Read the result

Method 3: Mental math for special numbers

• Numbers ending in 5: 25² = (2 × 3) hundred + 25 = 625

• Numbers ending in 0: 30² = (3 × 3) hundred = 900

• Nearby known squares: 19² is just below 20² = 400, so estimate around 361

Method 4: Pattern recognition

• Perfect squares increase by odd numbers: 1, 4, 9, 16, 25 (differences are 3, 5, 7, 9...)

• Use this to extend patterns mentally

Squaring Whole Numbers, Decimals, and Negatives

Different types of numbers follow specific rules when squared:

Whole numbers:

• Always produce positive results

• 8² = 64 (straightforward multiplication)

Decimal numbers:

• Multiply as usual, counting decimal places

• 1.5² = 1.5 × 1.5 = 2.25

• 0.3² = 0.3 × 0.3 = 0.09

Negative numbers:

• Squaring a negative always gives a positive result

• (-4)² = (-4) × (-4) = +16

• This is because negative × negative = positive

• Important: Be careful with notation—(-5)² = 25, but -5² = -25

Fractions:

• Square both numerator and denominator

• (3/4)² = 9/16

• (2/5)² = 4/25

Common Questions Students Ask About Squared Numbers

Why is exponent 2 called "squared"?

The term comes from geometry. When you calculate the area of a square with side length s, you multiply s × s, which we write as s². The visual connection between squaring numbers and square shapes gave us this terminology. Early mathematicians noticed that arranging objects in square grids required multiplying a number by itself.

Can a square be negative?

No—when you square any real number (positive or negative), the result is always positive or zero. This happens because multiplying two numbers with the same sign always produces a positive result. For example, (-3)² = +9 because negative times negative equals positive. The only number that squares to zero is zero itself: 0² = 0.

Why do squared numbers grow so quickly?

Squared numbers grow rapidly because you're multiplying the entire value by itself, not just doubling it. When you double a number, its square quadruples. For instance, 2² = 4, but 4² = 16 (four times larger, not twice). This exponential growth pattern explains why small increases in measurements lead to large increases in area, and why doubling your driving speed requires four times the stopping distance.

Conclusion

Understanding what does squared mean in math is essential for success in algebra, geometry, and applied mathematics. Squaring—multiplying a number by itself and representing it with the exponent 2—appears throughout mathematical formulas, real-world calculations, and problem-solving situations. Whether you're calculating area, working with the Pythagorean theorem, or analyzing growth patterns, knowing how to recognize the ² symbol and perform squaring operations builds your mathematical foundation.

Start practicing with small whole numbers to build confidence, then gradually work with decimals and fractions. Remember that squared numbers are always non-negative, grow quickly, and have an inverse relationship with square roots. The more comfortable you become with squaring, the easier you'll find advanced math topics.

Ready to master more essential math concepts? Explore HYE Tutors for clear, student-friendly guides on exponents, algebra fundamentals, and mathematical reasoning designed to help you succeed.