What Is Volume in Math?

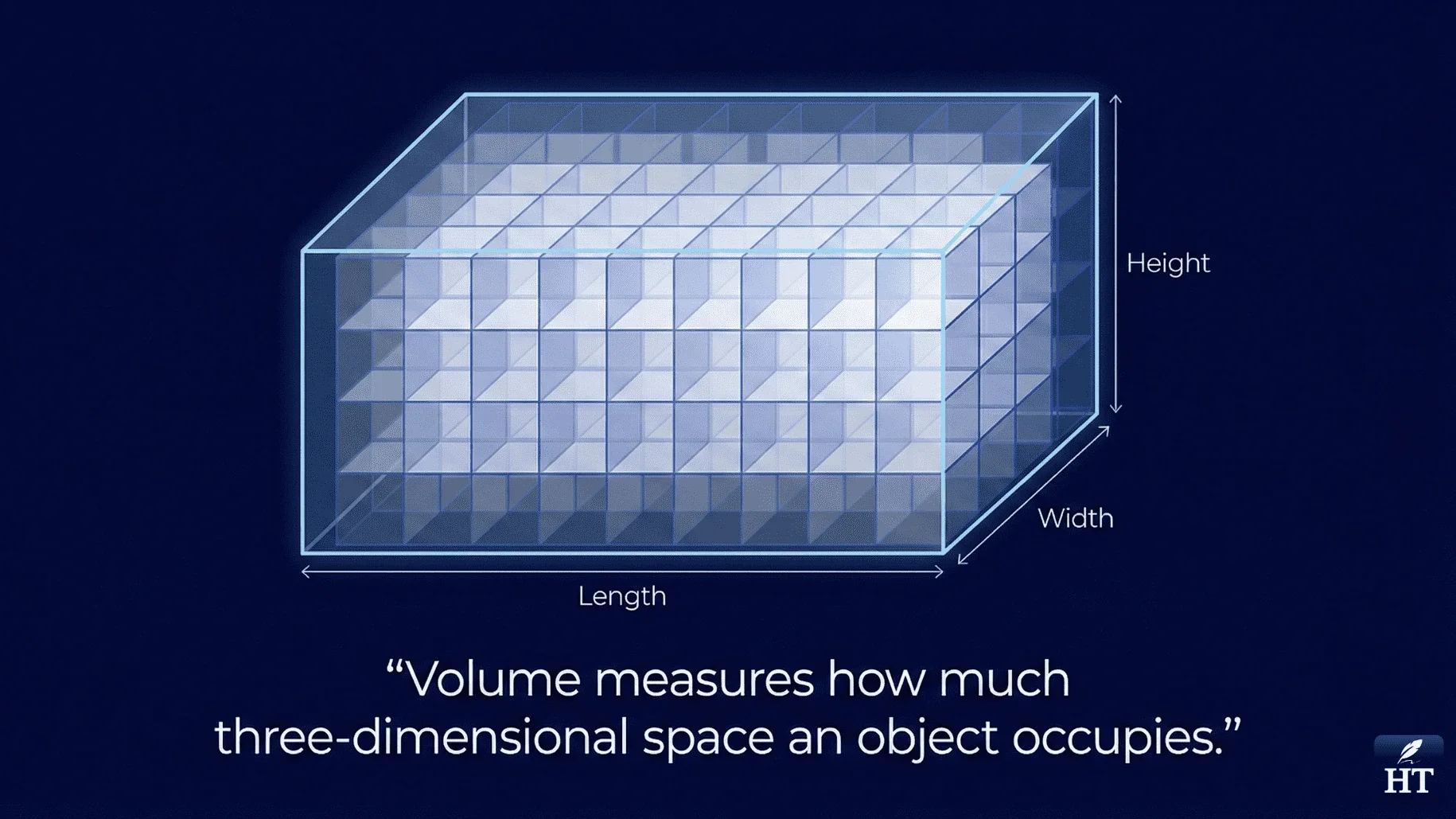
If you've ever wondered what is volume in math, you're exploring one of geometry's most practical concepts. Students often struggle to understand how volume differs from area, which formulas apply to different shapes, and how to calculate volume correctly for real-world objects. Simply put, volume measures how much three-dimensional space an object occupies—imagine filling a box with water or packing a shipping container with smaller boxes.

This comprehensive guide will explain volume clearly, provide formulas for common 3D shapes like cubes, cylinders, and spheres, walk through step-by-step calculations, and show you how to use volume calculators effectively. You'll also discover real-life connections that make this concept meaningful and practical. Whether you're calculating how much water fits in a pool or determining storage capacity, understanding volume is an essential math skill. Let's explore the formulas, examples, and applications together.

“Volume in math is the amount of space a 3D object occupies. It is measured in cubic units and calculated using formulas based on the shape, such as V = length × width × height for a box or V = πr²h for a cylinder. Volume tells us how much a container can hold or how much space an object takes up.”

— HYE Tutors

What Is Volume in Math?

Volume in math is the amount of three-dimensional space inside a 3D object. It tells you how much a container can hold or how much space a solid object takes up. Unlike area, which measures flat surfaces, volume specifically applies to objects with length, width, and height.

When students ask "what is the definition of volume in math" or "what is volume in math terms," the answer is always about measuring the interior capacity of three-dimensional shapes. Volume is expressed in cubic units because you're measuring space in three dimensions.

Real-world examples of volume:

• A water bottle holds 500 milliliters (500 cm³) of liquid

• A storage box might have a volume of 1,000 cubic inches

• An aquarium tank contains a specific number of gallons or liters

Volume vs. Area—Understanding the Difference:

Concept	Dimensions	Units	Example
Area	2D (length × width)	Square units (cm², m²)	Floor space in a room
Volume	3D (length × width × height)	Cubic units (cm³, m³)	Water in a swimming pool

Understanding what is the meaning of volume in math helps you solve problems involving containers, buildings, packaging, and natural objects.

Key Points to Remember About Volume

• Measures three-dimensional space – Volume only applies to 3D objects, not flat shapes

• Always uses cubic units – cm³, m³, liters, gallons, or cubic feet

• Requires three measurements – Usually length, width, and height (though formulas vary)

• Different formulas for different shapes – Cubes, cylinders, and spheres each have unique volume formulas

• Practical and measurable – You can physically measure volume by displacement or calculation

• Essential in science and daily life – Used in chemistry, physics, engineering, cooking, and construction

How Volume Works

Think of volume as counting how many identical cubes could fit inside a three-dimensional object. If you had a large box and filled it completely with one-centimeter cubes, the total number of cubes would equal the box's volume in cubic centimeters.

Visual concept: Imagine stacking blocks to fill a container. If you place 5 blocks along the length, 4 blocks along the width, and 3 blocks for height, you'd have 5 × 4 × 3 = 60 blocks total—that's 60 cubic units of volume.

How changing dimensions affects volume:

• Doubling the height doubles the volume (twice as much space)

• Doubling all dimensions increases volume by 8 times (2 × 2 × 2)

• Making a box taller increases volume proportionally to the height increase

Volume measurements help us understand capacity—how much liquid a pitcher holds, how much soil fits in a planter, or how many items can fit in a shipping container.

Why Volume Is Important in Math and Real Life

Understanding volume has countless practical applications:

• Construction and architecture – Calculating concrete needed for foundations or determining room capacity

• Container design – Creating bottles, boxes, and tanks that hold specific amounts

• Science experiments – Measuring liquid volumes in chemistry and biology

• Packaging and shipping – Determining how many products fit in boxes and trucks

• Storage solutions – Figuring out closet, garage, or warehouse capacity

• Cooking and baking – Following recipes that require specific liquid or ingredient volumes

• Environmental science – Measuring water reservoirs, rainfall collection, or pollution dispersion

Volume Formulas for Common 3D Shapes

Different three-dimensional shapes require different formulas to calculate volume. Understanding what is volume in math formula terms means knowing which formula matches each shape. Here are the most common formulas students encounter:

Shape	Volume Formula	Variables
Cube	V = s³	s = side length
Rectangular Prism	V = l × w × h	l = length, w = width, h = height
Cylinder	V = πr²h	r = radius, h = height
Sphere	V = (4/3)πr³	r = radius
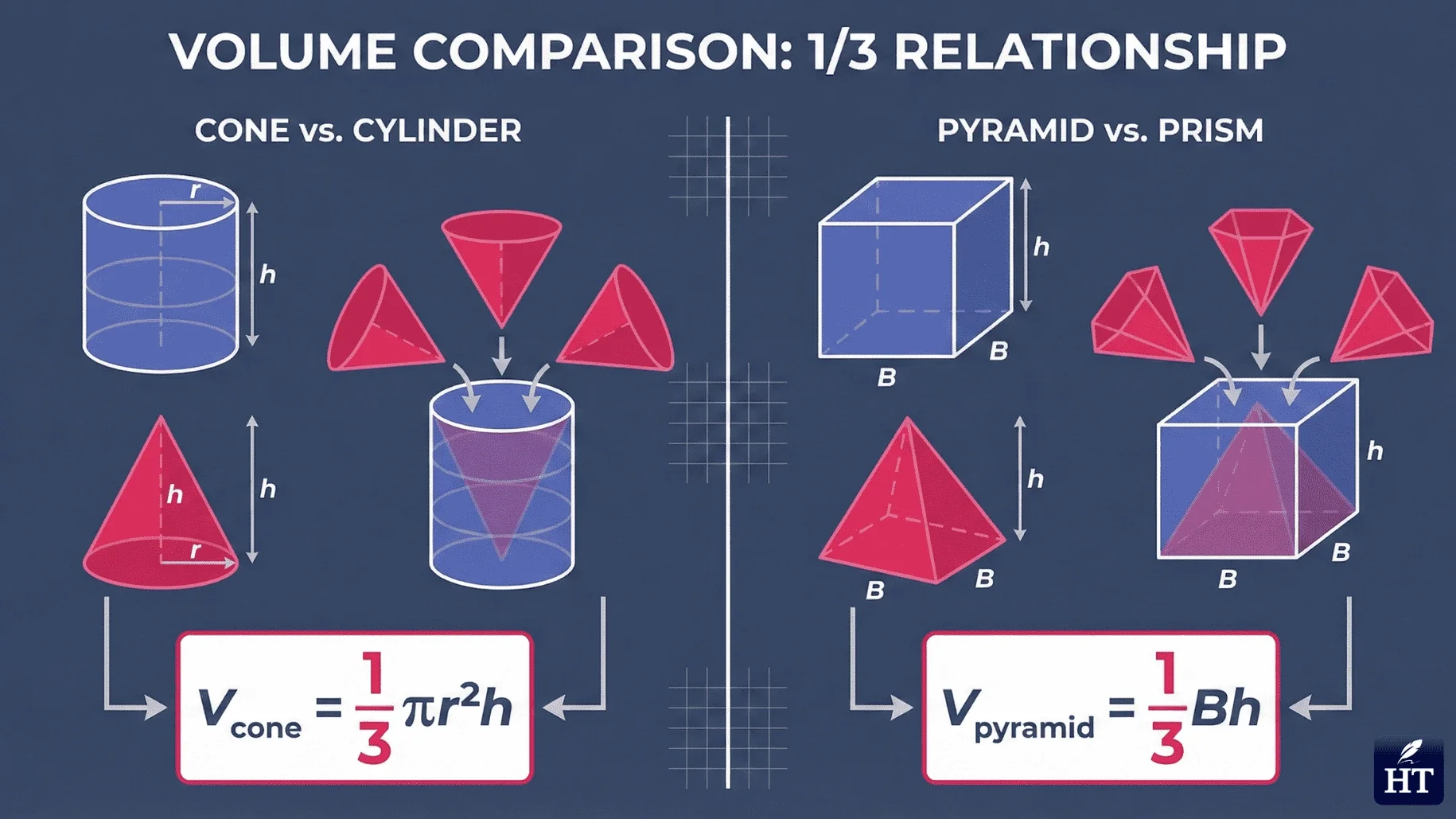
Cone	V = (1/3)πr²h	r = radius, h = height
Pyramid	V = (1/3) × base area × h	h = height

Important note on units: Volume is always measured in cubic units—cm³ (cubic centimeters), m³ (cubic meters), or converted units like liters. One liter equals 1,000 cm³, and one cubic meter equals 1,000 liters.

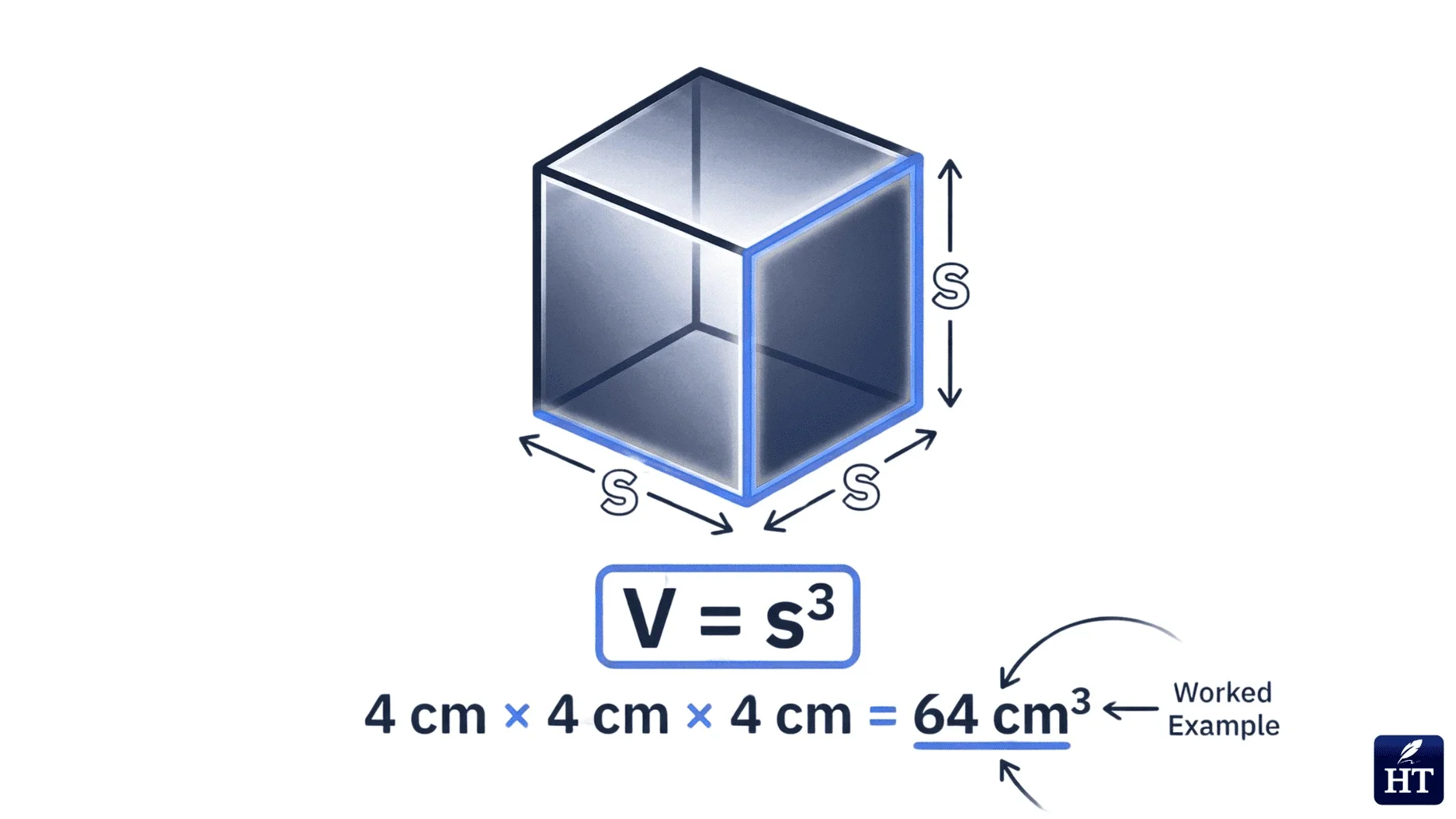
Cube Volume Formula

Formula: V = s³ (where s is the side length)

A cube has equal length, width, and height, so you multiply the side length by itself three times.

Example: A cube with 4 cm sides has a volume of:

• V = 4³ = 4 × 4 × 4 = 64 cm³

This is what is the formula for volume in math when all sides are equal.

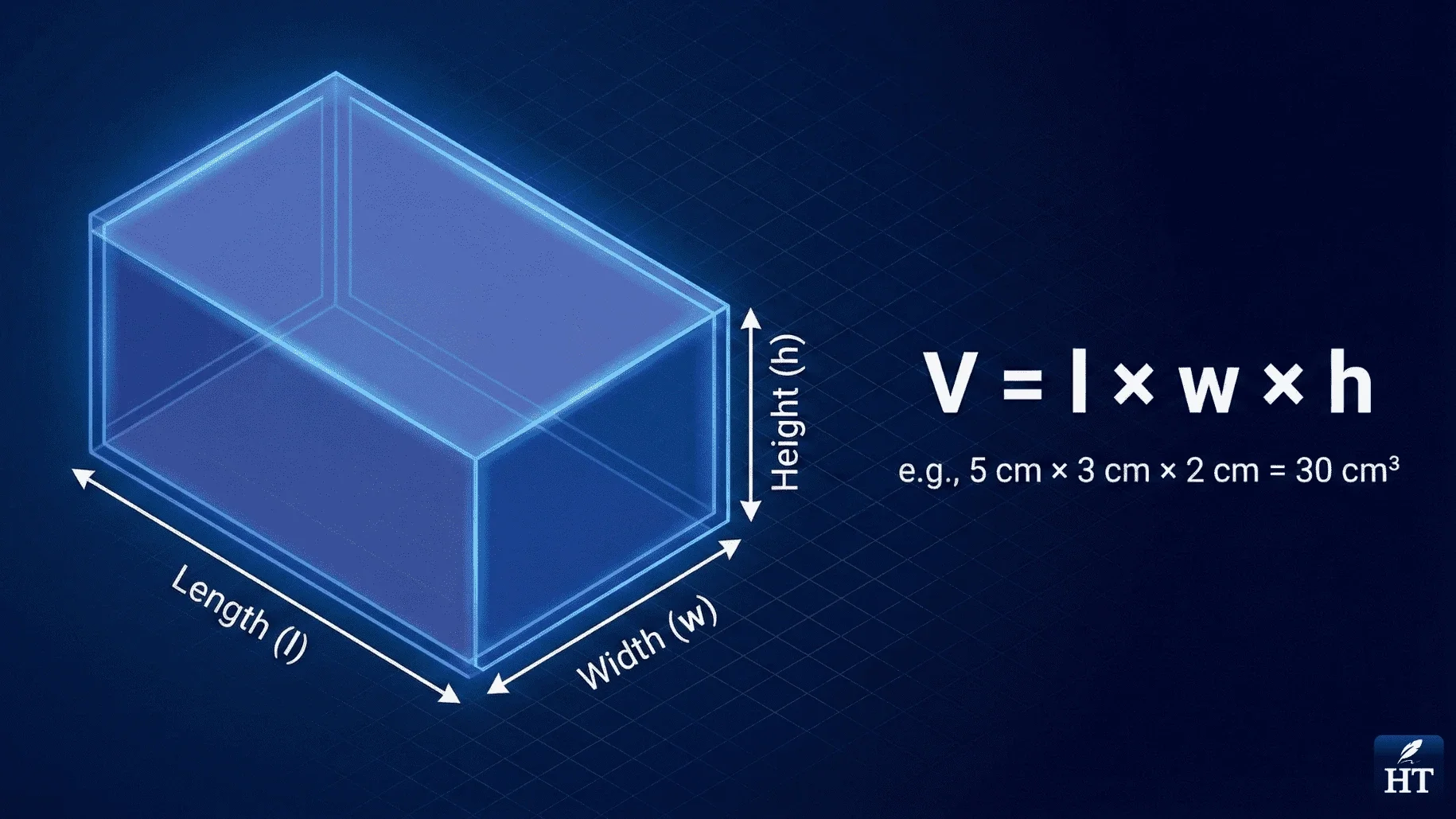
Rectangular Prism Volume Formula

Formula: V = l × w × h (length × width × height)

Also called a "box" shape, this is the most common volume calculation students encounter.

Example: A box measuring 6 inches long, 4 inches wide, and 3 inches tall:

• V = 6 × 4 × 3 = 72 cubic inches

This shape appears in storage boxes, rooms, and rectangular containers.

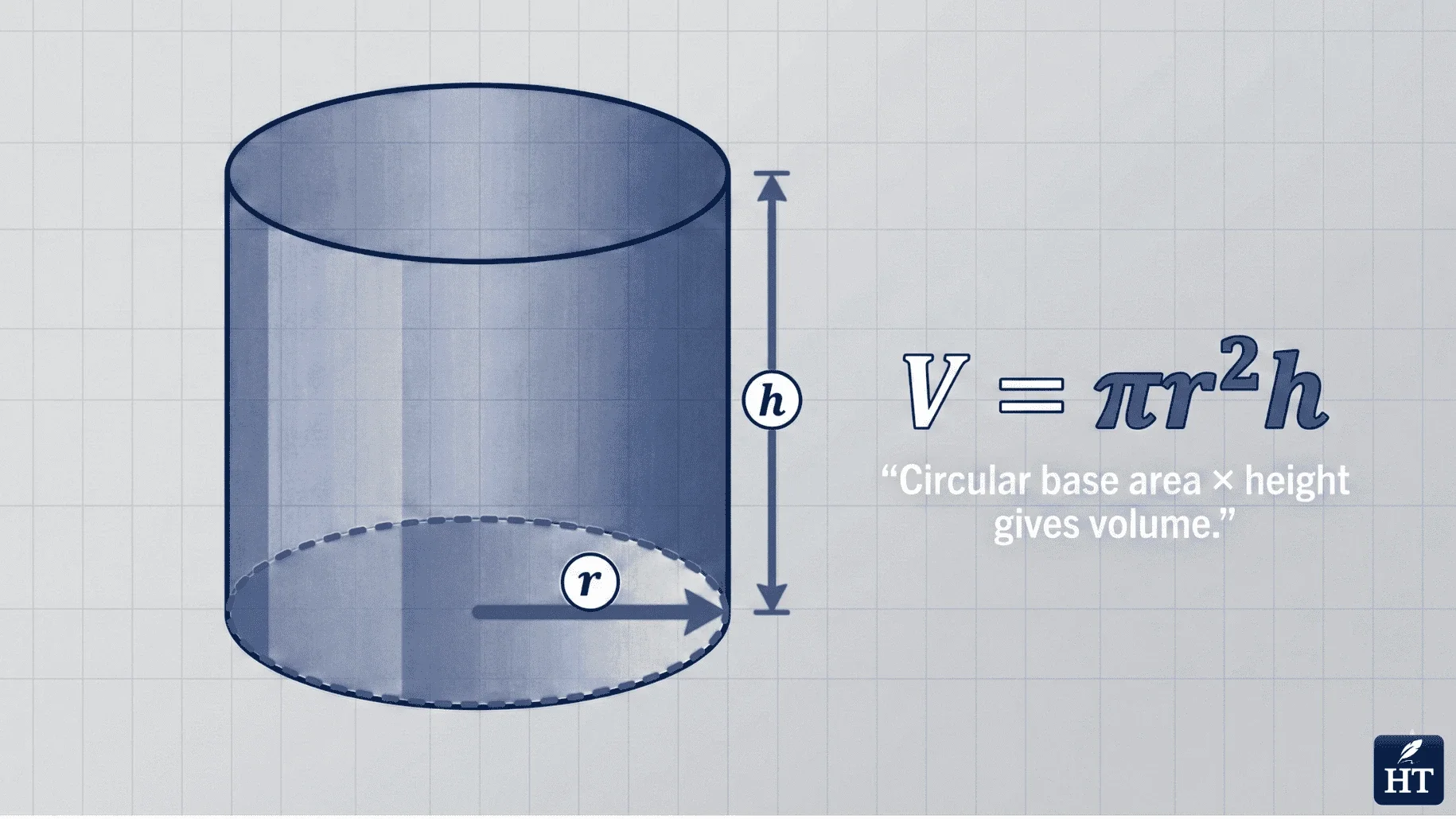
Cylinder Volume Formula

Formula: V = πr²h (where r is the radius and h is height)

The formula uses pi (π ≈ 3.14159) because the base is circular. You calculate the circle's area (πr²) and multiply by height.

Example: A cylinder with radius 3 cm and height 10 cm:

• V = π × 3² × 10

• V = π × 9 × 10

• V ≈ 3.14 × 90 ≈ 282.6 cm³

Cylinders appear in cans, pipes, drinking glasses, and storage tanks.

Sphere Volume Formula

Formula: V = (4/3)πr³ (where r is the radius)

This formula calculates the space inside a perfect ball shape. The (4/3) fraction comes from mathematical derivation involving circles and rotation.

Example: A sphere with radius 5 cm:

• V = (4/3) × π × 5³

• V = (4/3) × π × 125

• V ≈ 1.33 × 3.14 × 125 ≈ 523.3 cm³

Spheres appear in balls, globes, bubbles, and planets.

Cone & Pyramid Volume Formulas

Both cones and pyramids use the (1/3) fraction because they taper to a point, containing exactly one-third the volume of a cylinder or prism with the same base and height.

Cone formula: V = (1/3)πr²h Pyramid formula: V = (1/3) × base area × h

Example (Cone): A cone with radius 4 cm and height 9 cm:

• V = (1/3) × π × 4² × 9

• V = (1/3) × 3.14 × 16 × 9 ≈ 150.7 cm³

Think of these shapes as fractions of complete prisms—they hold one-third as much.

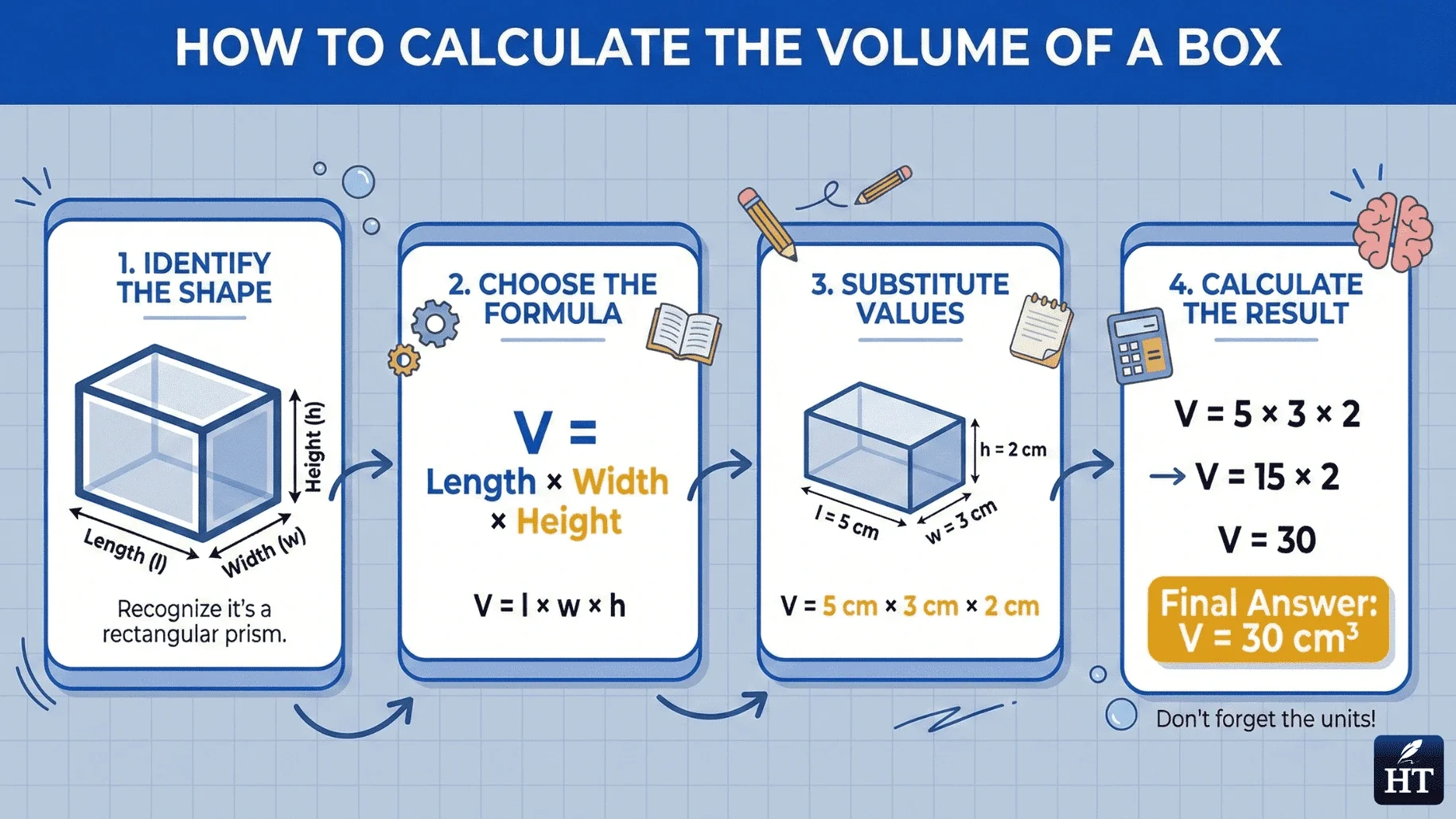
How to Calculate Volume Step by Step

When tackling any volume in math problem, follow this universal approach:

Step 1: Identify the shape Determine if you're working with a cube, prism, cylinder, sphere, cone, or pyramid.

Step 2: Measure all necessary dimensions Gather the measurements you need: side lengths, radius, height, or base area.

Step 3: Choose the correct formula Match your shape to its specific volume formula from the list above.

Step 4: Substitute values into the formula Replace variables with your actual measurements, keeping units consistent.

Step 5: Perform the calculations Multiply, apply exponents, and use π where needed (3.14 is usually sufficient).

Step 6: Check your units Ensure your answer is in cubic units (cm³, m³, etc.) that match your measurements.

Common mistakes to avoid:

• Using diameter instead of radius for circles

• Mixing different units (inches and feet together)

• Forgetting to cube or square numbers where required

• Confusing area formulas with volume formulas

• Using slant height instead of perpendicular height

Example: Finding the Volume of a Box

Let's calculate the volume of a rectangular storage box step-by-step:

Given measurements:

• Length = 12 inches

• Width = 8 inches

• Height = 5 inches

Solution:

1. Identify the shape: Rectangular prism

2. Use the formula: V = l × w × h

3. Substitute: V = 12 × 8 × 5

4. Calculate: V = 480

5. Add units: V = 480 cubic inches

This box can hold 480 cubic inches of items.

Volume Calculator Instructions

Using a volume calculator simplifies complex calculations, especially for shapes involving π:

Step 1: Select the 3D shape from the dropdown menu (cube, cylinder, sphere, etc.) 

Step 2: Enter the required dimensions in the input fields (radius, height, side length) 

Step 3: Ensure all measurements use the same units 

Step 4: Click "Calculate" to get the volume result 

Step 5: Note the units in your answer (the calculator should display cm³, m³, or your chosen unit)

Online calculators are helpful for checking homework answers and handling decimals accurately.

Real-Life Examples of Volume

Understanding what is volume in math becomes practical when you see everyday applications:

Swimming pool capacity

• An above-ground pool measuring 12 feet long, 8 feet wide, and 4 feet deep

• Volume = 12 × 8 × 4 = 384 cubic feet (approximately 2,870 gallons of water)

Water storage tank

• A cylindrical tank with 3-meter radius and 5-meter height

• Volume = π × 3² × 5 ≈ 141.3 m³ (or 141,300 liters)

Shipping box optimization

• A box 20 cm × 15 cm × 10 cm holds 3,000 cm³

• Doubling the height increases volume to 6,000 cm³ (twice as much fits inside)

Beverage containers

• A soda can (cylinder) with 3 cm radius and 12 cm height holds about 339 cm³ (339 mL)

Moving truck capacity

• A truck cargo area 10 ft × 6 ft × 7 ft = 420 cubic feet of storage space

These examples show how changing dimensions directly impacts how much fits inside—critical for planning, purchasing, and problem-solving.

Volume Units Explained

Volume uses cubic units because you're measuring three dimensions multiplied together.

Common volume units:

• cm³ (cubic centimeters) – Small objects, laboratory measurements

• m³ (cubic meters) – Large spaces, rooms, pools

• Liters – Liquids (1 liter = 1,000 cm³)

• Milliliters (mL) – Small liquid amounts (1 mL = 1 cm³)

Quick conversions:

• 1 m³ = 1,000 liters

• 1 liter = 1,000 cm³

• 1 cubic foot ≈ 28.3 liters

Always ensure your measurements and final answer use matching units.

Practice Problems with Quick Answers

Test your understanding of volume calculations:

Problem 1: Find the volume of a cube with 6 cm sides. Answer: V = 6³ = 216 cm³

Problem 2: Calculate the volume of a rectangular prism: 10 cm × 5 cm × 4 cm. Answer: V = 10 × 5 × 4 = 200 cm³

Problem 3: What is the volume of a cylinder with radius 2 cm and height 8 cm? Answer: V = π × 2² × 8 ≈ 100.5 cm³

Problem 4: Find the volume of a sphere with radius 3 cm. Answer: V = (4/3) × π × 3³ ≈ 113.1 cm³

Problem 5: Calculate the volume of a cone with radius 5 cm and height 12 cm. Answer: V = (1/3) × π × 5² × 12 ≈ 314.2 cm³

Problem 6: A box is 15 inches × 10 inches × 8 inches. What's its volume? Answer: V = 15 × 10 × 8 = 1,200 cubic inches

Problem 7: If a cubic storage unit has 4-foot sides, what's its volume? Answer: V = 4³ = 64 cubic feet

Common Misconceptions About Volume

Students often make these mistakes when learning about volume:

• Confusing area with volume – Area is 2D (square units); volume is 3D (cubic units)

• Using wrong units – Forgetting to cube the units or mixing different measurement systems

• Choosing incorrect formulas – Applying a cube formula to a cylinder or vice versa

• Forgetting π in circular shapes – Cylinders, cones, and spheres require π in their formulas

• Using diameter instead of radius – Formulas use radius (half the diameter), not the full diameter

• Confusing height types – Some shapes use perpendicular height, not slant height

• Skipping the one-third fraction – Cones and pyramids need the (1/3) multiplier

Double-checking which formula matches your shape prevents most calculation errors.

Conclusion

Understanding what is volume in math empowers you to solve real-world problems involving space, capacity, and three-dimensional measurements. Whether you're calculating how much water fills a pool, determining storage container sizes, or working through geometry homework, volume formulas provide the tools you need. Remember that volume always involves three dimensions, uses cubic units, and varies by shape—cubes, cylinders, spheres, and pyramids each have their own specific formulas.

Practice with different shapes builds confidence and accuracy. Start with simple rectangular prisms, then progress to cylinders and spheres as you become more comfortable. The more you work with these formulas, the more naturally you'll recognize which one applies to each situation.

Ready to explore more geometry concepts? Visit HYE Tutors for comprehensive guides on area calculations, 3D shapes, and measurement units designed to strengthen your mathematical skills

References:

• Khan Academy: Volume of 3D Shapes – Comprehensive video lessons and practice problems

• National Council of Teachers of Mathematics – Teaching standards for measurement concepts

• Math is Fun: Volume Calculator – Interactive calculator with multiple shapes