What Is Order of Operations in Math? Complete Guide
If you've ever wondered what is the order of operations in math, you're not alone. Students frequently encounter problems where they perform the correct arithmetic but still get the wrong answer—usually because they solved operations in the incorrect sequence. The order of operations is a fundamental set of rules that ensures everyone solves math problems the same way and arrives at the same correct answer.
This complete guide will explain the definition clearly, teach you the correct sequence using PEMDAS, walk through step-by-step examples, identify common mistakes, and provide practice problems with solutions. Whether you're working with brackets, exponents, fractions, or mixed operations, understanding these rules is essential for success in algebra, equations, and advanced mathematics. By the end of this guide, you'll have the confidence to tackle complex expressions accurately and consistently. Let's explore how these rules work and why they matter.
“The order of operations in math is a set of rules that tells us the correct sequence to solve math problems with multiple operations. The correct order is: parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right). Following the order of operations ensures everyone gets the same correct answer.”
What Is the Order of Operations in Math?
The order of operations in math is a standardized set of rules that determines which calculations to perform first when an expression contains multiple operations. Without these rules, the same math problem could have different answers depending on how someone chose to solve it.
You might also search for "what is the order of operation in math" or "in math what is the order of operations"—all refer to the same essential concept. The definition of order of operations in math is: a hierarchy of mathematical operations that must be followed in sequence to ensure accurate, consistent results.
Why the order matters: Consider the expression: 6 + 3 × 2
If you work left to right: (6 + 3) × 2 = 9 × 2 = 18 ❌
Using correct order: 6 + (3 × 2) = 6 + 6 = 12 ✓
The second answer is correct because multiplication must happen before addition. Without standardized rules, mathematical communication would be chaotic and unreliable.
Order of Operations in Simple Terms
Understanding the order of operations becomes easier with these key principles:
Operations have priority levels – Some operations must be completed before others, regardless of their position in the expression
Work from strongest to weakest – Parentheses are strongest, followed by exponents, then multiplication/division, and finally addition/subtraction
Equal-priority operations go left to right – When operations have the same priority (like multiplication and division), solve them in the order they appear from left to right
Grouping symbols create mini-problems – Anything inside parentheses, brackets, or above/below fraction bars gets solved first as its own separate calculation
What Is the Correct Order of Operations in Math?
Understanding what is the correct order of operations in math is crucial for solving expressions accurately. The standard sequence has been agreed upon by mathematicians worldwide to ensure consistency in problem-solving.
The key to mastering this concept is recognizing that some operations share the same priority level and must be solved from left to right when they appear together. This prevents confusion and ensures standardized results across all mathematical contexts.
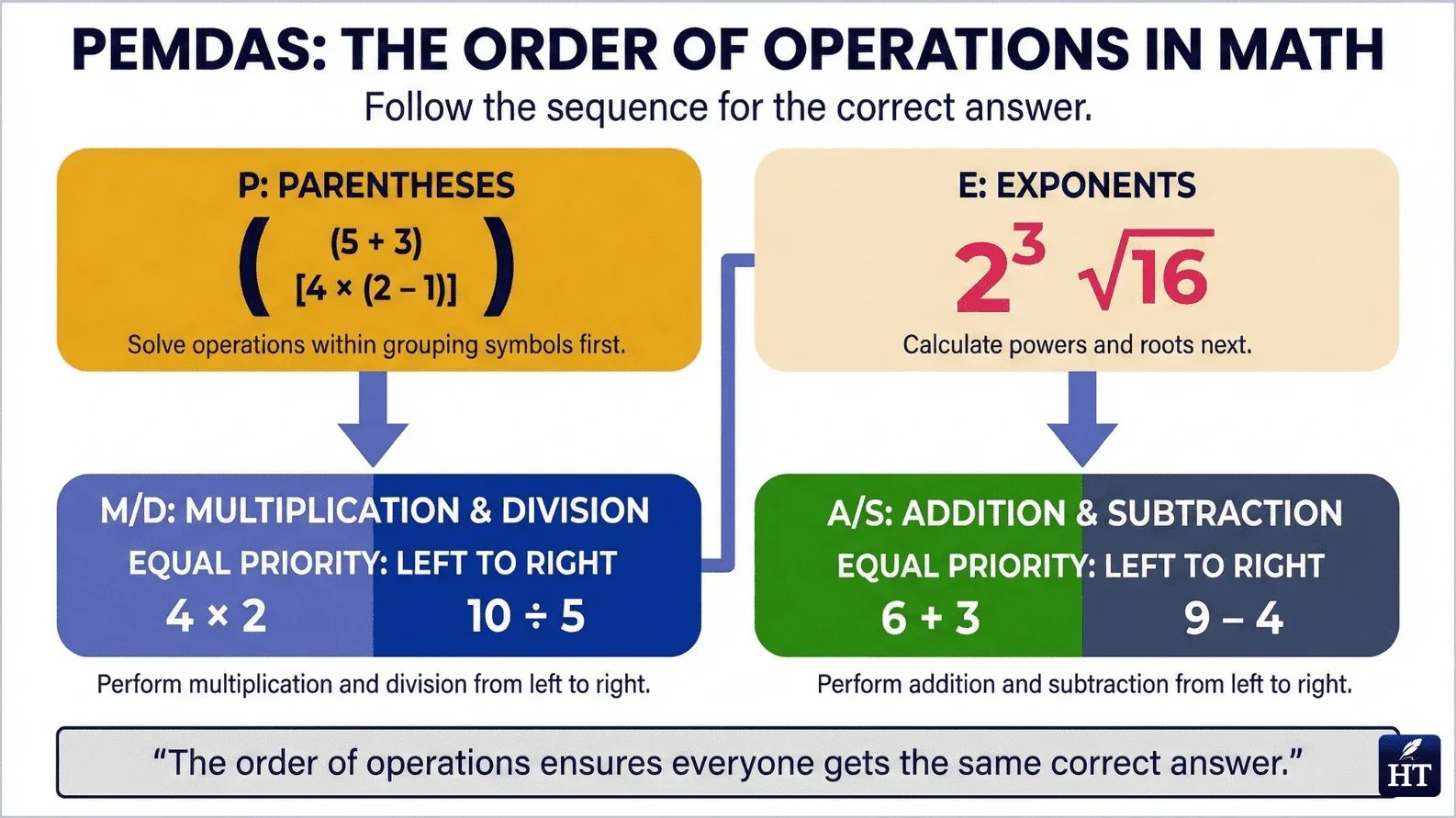
The Correct Order (PEMDAS Rule)
Follow this sequence when solving any mathematical expression:
Parentheses – Solve everything inside grouping symbols first (parentheses, brackets, braces)
Exponents – Calculate all powers and roots next
Multiplication and Division – Work from left to right (these share equal priority)
Addition and Subtraction – Work from left to right (these share equal priority)
Critical understanding: Multiplication does NOT always come before division, and addition does NOT always come before subtraction. When operations share the same level, you must solve them in the order they appear from left to right.
Why Multiplication Comes Before Addition
Multiplication represents repeated addition, making it a "stronger" operation that groups numbers together. When we write 5 + 3 × 4, the multiplication sign tells us that 3 and 4 are bound together as a group (12), which then gets added to 5.
Think of it this way: multiplication and division create the building blocks, while addition and subtraction combine or separate those blocks. The structure must be built before it can be assembled, which is why multiplication and division happen before addition and subtraction.
This hierarchy reflects how mathematical expressions represent real-world relationships and ensures formulas work correctly in science, engineering, and everyday calculations.
What Does PEMDAS Mean?
PEMDAS is a popular memory device (mnemonic) that helps students remember the order of operations in math. Each letter represents one step in the sequence, making it easier to recall the correct order when solving problems.
PEMDAS stands for:
P – Parentheses
E – Exponents
M – Multiplication
D – Division
A – Addition
S – Subtraction
Alternative mnemonics include "Please Excuse My Dear Aunt Sally" to help remember the letters in order.
Important clarification: While PEMDAS lists multiplication before division and addition before subtraction, these pairs actually have equal priority. You must solve multiplication and division from left to right as they appear, and do the same with addition and subtraction.
PEMDAS Breakdown (With Meaning)
Parentheses (P) – Solve all operations inside grouping symbols first, working from innermost to outermost
Exponents (E) – Calculate all powers (like 5²) and roots (like √16) next
Multiplication (M) and Division (D) – These share equal priority; solve whichever comes first from left to right
Addition (A) and Subtraction (S) – These share equal priority; solve whichever comes first from left to right
Common PEMDAS Misunderstandings
❌ WRONG: "Multiplication always comes before division" ✓ CORRECT: Multiplication and division have equal priority—solve from left to right
Example: 12 ÷ 3 × 2
Wrong approach: 12 ÷ (3 × 2) = 12 ÷ 6 = 2 ❌
Correct approach: (12 ÷ 3) × 2 = 4 × 2 = 8 ✓
❌ WRONG: "Addition always comes before subtraction" ✓ CORRECT: Addition and subtraction have equal priority—solve from left to right
Example: 10 - 3 + 2
Wrong approach: 10 - (3 + 2) = 10 - 5 = 5 ❌
Correct approach: (10 - 3) + 2 = 7 + 2 = 9 ✓
Order of Operations in Math Problems (Step-by-Step)
Let's walk through how to apply the order of operations in math problems using a comprehensive example. Following these steps systematically ensures accuracy every time.
Example Problem: 3 + 2² × (8 - 3) ÷ 5
We'll solve this step-by-step, showing our work at each stage.
Step 1 — Solve Parentheses First
Always begin by calculating anything inside parentheses or other grouping symbols.
Original: 3 + 2² × (8 - 3) ÷ 5 Calculate: 8 - 3 = 5 Result: 3 + 2² × 5 ÷ 5
Step 2 — Handle Exponents
After parentheses are resolved, calculate all exponents (powers and roots).
Current: 3 + 2² × 5 ÷ 5 Calculate: 2² = 2 × 2 = 4 Result: 3 + 4 × 5 ÷ 5
Step 3 — Multiply and Divide (Left to Right)
Now work through all multiplication and division operations as they appear from left to right.
Current: 3 + 4 × 5 ÷ 5 First: 4 × 5 = 20 Then: 20 ÷ 5 = 4 Result: 3 + 4
Step 4 — Add and Subtract (Left to Right)
Finally, complete all addition and subtraction operations from left to right.
Current: 3 + 4 Calculate: 3 + 4 = 7 Final Answer: 7
Complete solution summary: 3 + 2² × (8 - 3) ÷ 5 = 3 + 2² × 5 ÷ 5 = 3 + 4 × 5 ÷ 5 = 3 + 20 ÷ 5 = 3 + 4 = 7
Order of Operations in Math Equations
Students often ask "in a math equation what is the order of operations" and "what is the order of operations in math equations." The rules remain the same whether you're working with expressions or equations.
Key difference:
Expression: A mathematical phrase without an equals sign (e.g., 5 + 3 × 2)
Equation: A mathematical statement with an equals sign showing two expressions are equal (e.g., x + 5 = 12 or 3 + 2 × 4 = 11)
When solving equations, you apply the order of operations to simplify each side separately, then use inverse operations to solve for variables. The order of operations ensures you simplify correctly before isolating the variable.
Example equation: 2x + 3 × 4 = 20
Simplify the left side using order of operations:
First: 3 × 4 = 12
Then: 2x + 12 = 20
Finally solve: 2x = 8, so x = 4
Expressions vs Equations
| Feature | Expression | Equation |
|---|---|---|
| Equals sign | No | Yes |
| Purpose | Calculate a value | Show equality or solve for unknowns |
| Example | 6 + 3 × 2 | 6 + 3 × 2 = 12 |
| Order of operations | Apply to simplify | Apply to both sides before solving |
Understanding this distinction helps you recognize when to simplify versus when to solve for variables.
Order of Operations with Brackets, Fractions, and Exponents
More complex problems involve nested grouping symbols, fraction bars, and multiple exponents. Understanding how the order of operations applies in these situations is essential for advanced mathematics.
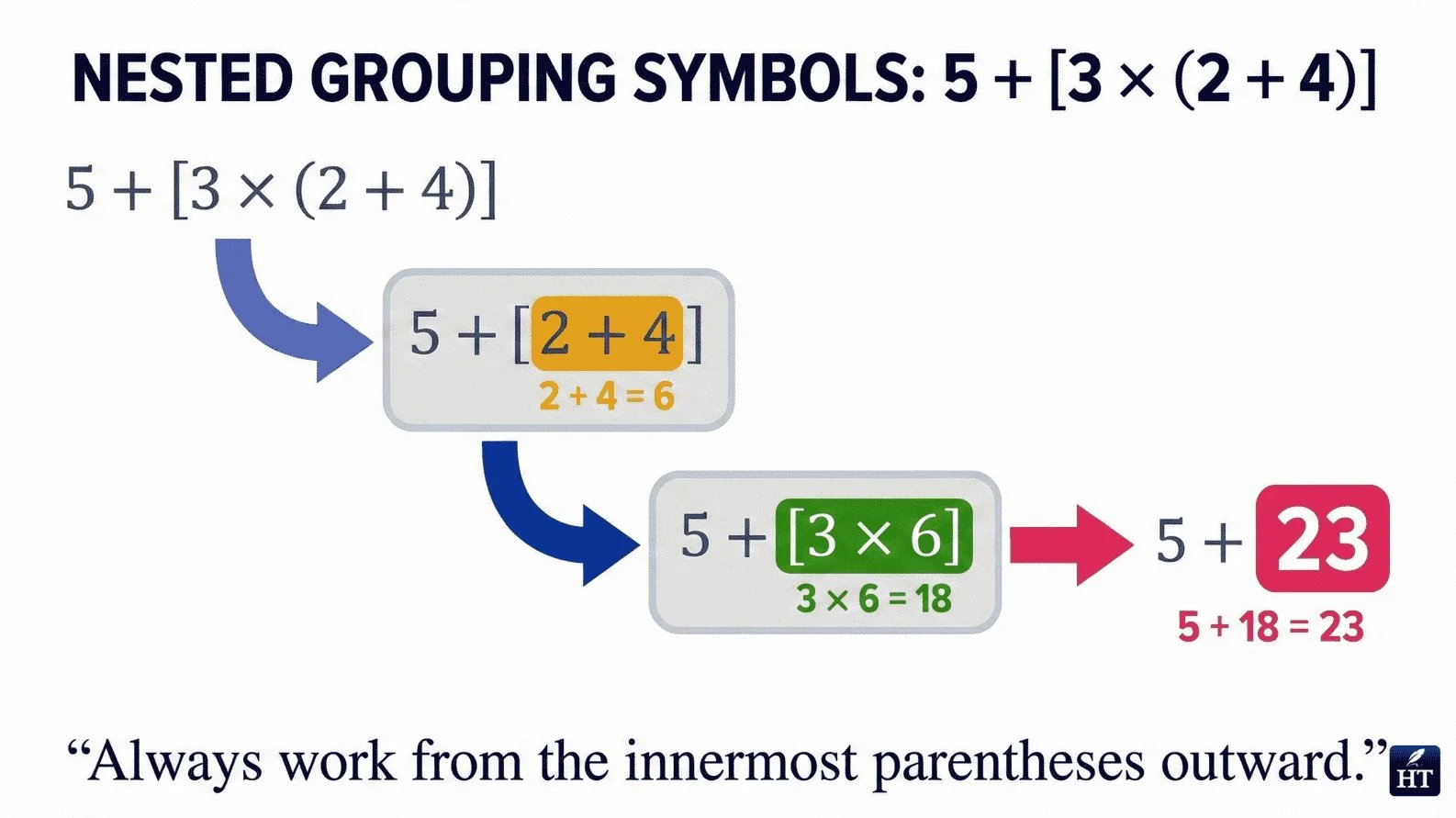
Multiple Parentheses and Nested Grouping
When parentheses are nested (one inside another), work from the innermost set outward.
Example: 5 + [3 × (2 + 4)]
Step 1: Innermost parentheses first: (2 + 4) = 6 Step 2: Next grouping: [3 × 6] = 18 Step 3: Final addition: 5 + 18 = 23
Grouping symbols from strongest to weakest:
Innermost parentheses ( )
Brackets [ ]
Braces { }
Some problems use multiple types: { [ ( ) ] }—always work inside-out.
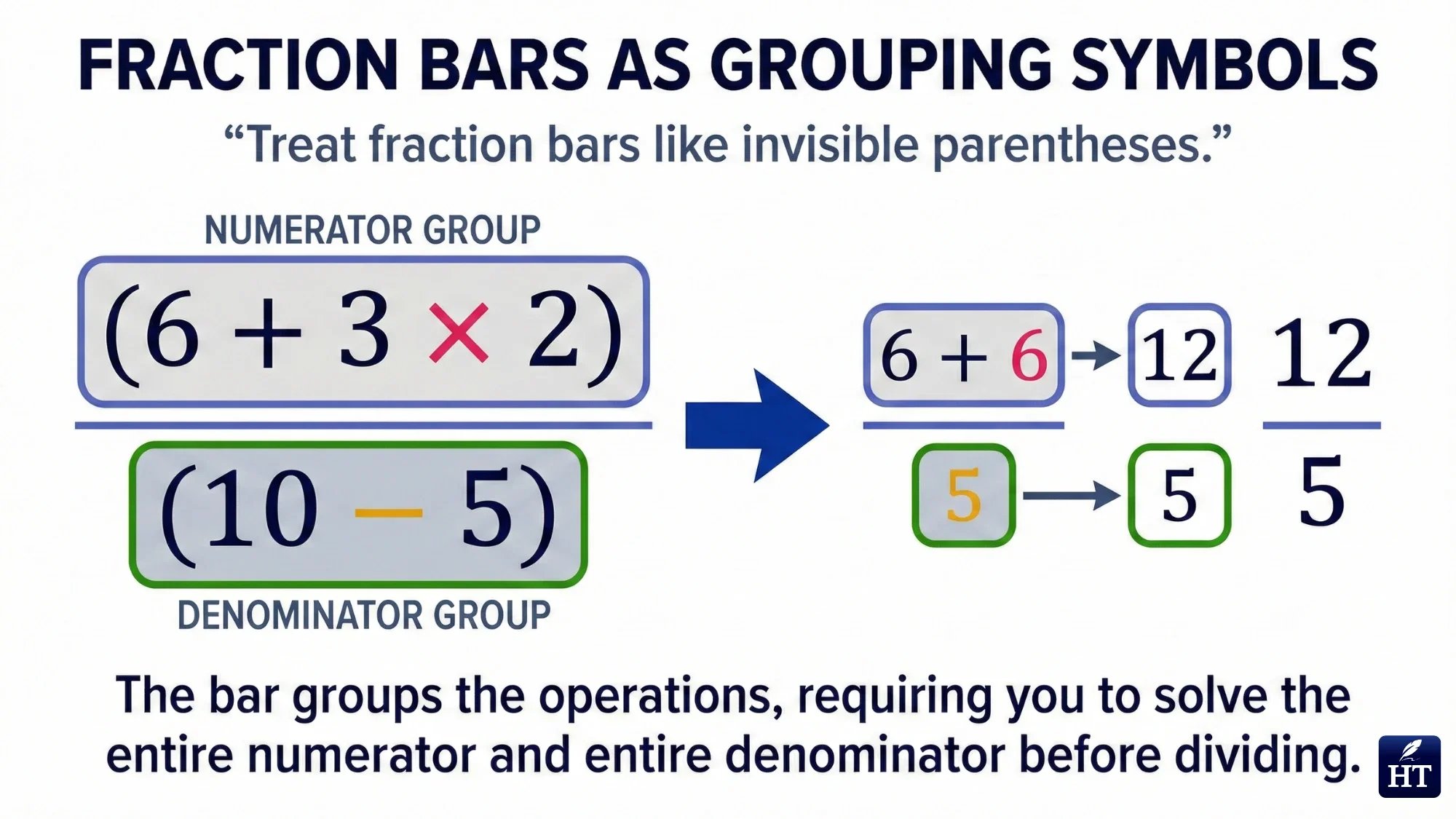
Fractions and the Order of Operations
Fraction bars act as grouping symbols—they group everything above and everything below separately.
Example: (6 + 3 × 2) / (10 - 5)
Step 1: Simplify the numerator using order of operations
6 + 3 × 2 = 6 + 6 = 12
Step 2: Simplify the denominator using order of operations
10 - 5 = 5
Step 3: Divide: 12 ÷ 5 = 2.4
Treat the numerator and denominator as if they each have invisible parentheses around them.
Working with multiple exponents:
When expressions contain several exponents, calculate them from left to right after handling all parentheses.
Example: 2³ + 5² - 4²
2³ = 8
5² = 25
4² = 16
Then: 8 + 25 - 16 = 17
Common Mistakes Students Make
Understanding frequent errors helps you avoid them in your own work:
Working strictly left to right without considering priority – Treating all operations as equal leads to wrong answers; you must follow the hierarchy
Ignoring or forgetting parentheses – Skipping grouping symbols changes the problem entirely
Misapplying PEMDAS as strict order – Thinking multiplication always comes before division or addition before subtraction
Calculating exponents incorrectly – Confusing -3² with (-3)² gives different results (-9 vs +9)
Not working through nested parentheses systematically – Jumping around instead of working inside-out creates errors
Forgetting that fraction bars are grouping symbols – Treating numerator and denominator operations independently instead of as grouped expressions
Rushing through problems – Skipping written steps makes it easy to lose track of which operations you've completed
Prevention strategy: Write out each step clearly, mark off operations as you complete them, and double-check your work using the PEMDAS sequence.
Practice Problems — Order of Operations
Test your understanding with these problems ranging from basic to more challenging:
Problem 1: 8 + 2 × 5 Answer: 8 + 10 = 18
Problem 2: (6 + 2) × 3 - 4 Answer: 8 × 3 - 4 = 24 - 4 = 20
Problem 3: 15 ÷ 3 + 2 × 4 Answer: 5 + 2 × 4 = 5 + 8 = 13
Problem 4: 3² + 2 × (5 - 1) Answer: 9 + 2 × 4 = 9 + 8 = 17
Problem 5: 20 - 12 ÷ 4 + 3 Answer: 20 - 3 + 3 = 17 + 3 = 20
Problem 6: 4 + 3 × 2² - 5 Answer: 4 + 3 × 4 - 5 = 4 + 12 - 5 = 11
Problem 7: (8 - 3) × 2 + 10 ÷ 5 Answer: 5 × 2 + 10 ÷ 5 = 10 + 2 = 12
Problem 8: 100 ÷ 5 ÷ 2 + 3 × 2 Answer: 20 ÷ 2 + 3 × 2 = 10 + 6 = 16
Practice these problems step-by-step, writing out each operation as you complete it. Check your answers and review any mistakes to strengthen your understanding.
Why the Order of Operations Matters in Math
The order of operations isn't just an arbitrary rule—it has practical importance across mathematics, science, technology, and everyday problem-solving.
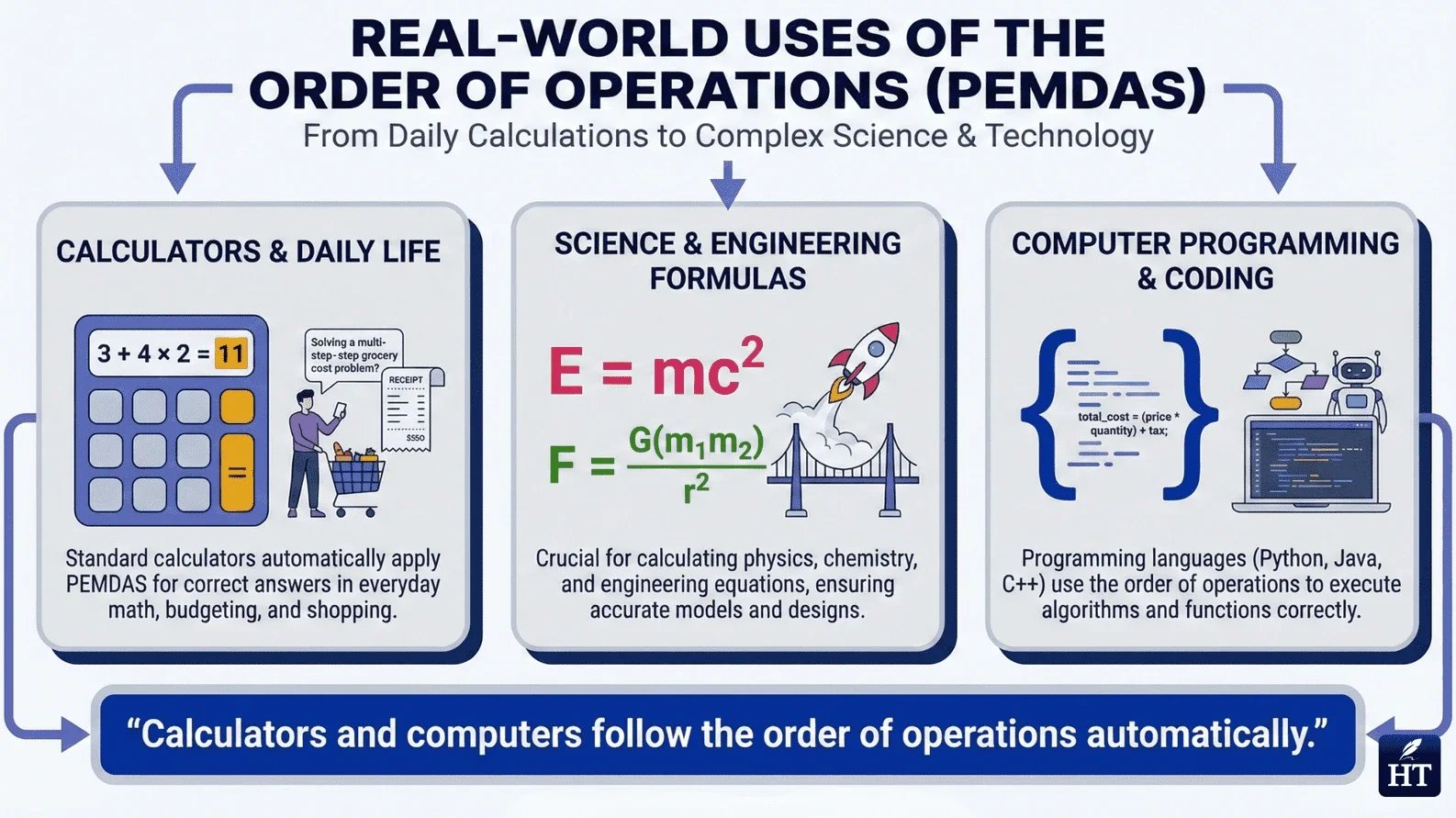
Standardization in communication: Mathematical formulas and expressions must mean the same thing to everyone who reads them. Scientists, engineers, and mathematicians worldwide follow the same rules, ensuring equations work consistently across languages and contexts.
Calculator and computer programming: Digital calculators and programming languages are coded to follow the order of operations automatically. When you enter an expression into a calculator or write code, the device applies PEMDAS rules to produce the correct result.
Scientific formulas: Physics, chemistry, and engineering formulas rely on the order of operations. For example, the kinetic energy formula KE = ½mv² requires squaring velocity before multiplying—doing operations out of order would give incorrect physical predictions.
Real-world problem solving: Calculating costs, measurements, distances, and financial projections often involves multiple operations that must be performed in the correct sequence for accurate results.
Understanding and applying the order of operations builds logical thinking skills and mathematical precision essential for academic success and practical applications.
FAQs — Frequently Asked Questions
What is the order of operations in math?
The order of operations in math is a set of rules determining which calculations to perform first in expressions with multiple operations. The sequence is: parentheses, exponents, multiplication and division (left to right), and addition and subtraction (left to right). This ensures everyone solves problems the same way and gets the same correct answer.
What is the correct order of operations in math?
The correct order of operations follows PEMDAS: Parentheses first, Exponents second, Multiplication and Division from left to right third, and Addition and Subtraction from left to right last. Remember that operations at the same level (like multiplication and division) are solved in the order they appear from left to right, not in a strict sequence.
Why do we use PEMDAS?
We use PEMDAS as a memory aid to remember the order of operations consistently. Without standardized rules, the same mathematical expression could have multiple different answers depending on how someone chose to solve it. PEMDAS ensures everyone follows the same sequence, making mathematical communication clear and reliable across all contexts.
Does division come before multiplication?
No—division does not always come before multiplication, and multiplication does not always come before division. They have equal priority in the order of operations. When both appear in the same expression, you solve them from left to right in whichever order they appear. For example, 12 ÷ 3 × 2 = 4 × 2 = 8.
How do you solve order of operations problems easily?
Solve order of operations problems systematically by working through PEMDAS step-by-step: handle all parentheses first, then exponents, then multiplication and division from left to right, and finally addition and subtraction from left to right. Write out each step clearly, mark off completed operations, and double-check your work to avoid rushing errors.
What happens if you ignore the order of operations?
Ignoring the order of operations leads to incorrect answers. For example, solving 6 + 3 × 2 from left to right gives (6 + 3) × 2 = 18, but the correct answer using proper order is 6 + (3 × 2) = 12. In real-world applications like engineering or programming, incorrect operation order can cause serious calculation errors with significant consequences.
Is the order of operations the same worldwide?
Yes, the order of operations is a universal mathematical convention used worldwide. While different countries may use different mnemonics (PEMDAS in the US, BODMAS in the UK, BIDMAS elsewhere), they all represent the same sequence of operations: brackets/parentheses, exponents/orders/indices, multiplication and division, addition and subtraction.
How is order of operations used in calculators?
Scientific and graphing calculators are programmed to follow the order of operations automatically. When you enter an expression, the calculator applies PEMDAS rules to determine which operations to perform first. However, basic four-function calculators typically work strictly left to right, so you must manually enter operations in the correct order when using them.
Conclusion
Mastering what is the order of operations in math transforms your ability to solve complex problems accurately and confidently. By following the PEMDAS sequence—parentheses, exponents, multiplication and division from left to right, addition and subtraction from left to right—you ensure consistent, correct results every time. This fundamental skill forms the foundation for success in algebra, equations, advanced mathematics, and real-world applications.
The more you practice applying these rules systematically, the more natural the process becomes. Start with simple expressions, gradually work up to problems involving nested parentheses and multiple exponents, and always check your work step-by-step. Remember that understanding why the order matters—not just memorizing PEMDAS—builds deeper mathematical reasoning.
Ready to strengthen your mathematical foundation? Explore HYE Tutors for comprehensive guides on algebraic expressions, solving equations, working with exponents, and fraction operations designed to build your confidence and skills
References
References
Khan Academy: Order of Operations – Comprehensive video lessons and practice exercises
Math is Fun: Order of Operations – Interactive examples and explanations
Purple Math: PEMDAS Explained – Detailed tutorial with common mistakes