How to Do Long Division — Step by Step Guide.
If you've ever searched how to do long division, you're not alone—this multi-step process frustrates many students and parents helping with homework. The confusion often comes from keeping track of multiple operations (divide, multiply, subtract, bring down), worrying about making mistakes, or not understanding when to stop. Perhaps you've watched someone solve a problem but still can't replicate the steps yourself, or maybe you need to help your child and feel rusty on the method.
This comprehensive guide will teach you how to do long division step by step with clear explanations, worked examples covering whole numbers, remainders, decimals, big numbers, fractions, variables, and polynomials, plus grade-specific tips for 4th and 5th graders. You'll find diagrams, practice problems, and common mistake fixes designed to build your confidence. Long division is a learnable skill—once you understand the pattern, you can apply it to any division problem. Let's break down the process together with examples you can use right away.
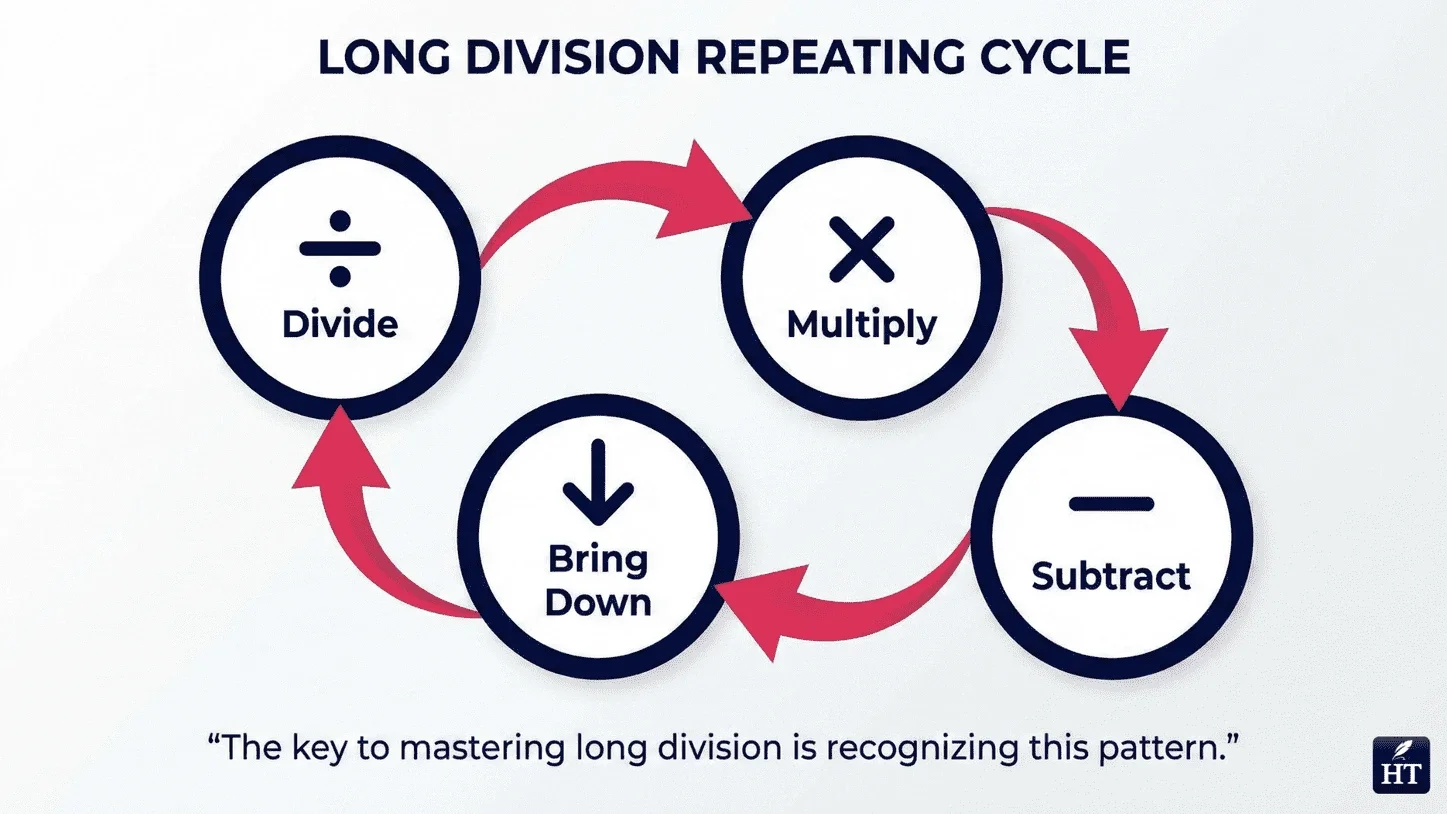
“Long division is a step-by-step method for dividing one number by another when the answer is not obvious. To do long division, follow this sequence:
✔ Divide The First Part of The Dividend by the Divisor
✔ Multiply The Divisor by The Result
✔ Subtract To Find the Remainder
✔ Bring Down the Next Digit, And
✔ Repeat Divide–Multiply–Subtract–Bring Down Until No Digits Are Left.
If there is a number left over, that’s the remainder. This method works for whole numbers, decimals, big numbers, and even polynomials
”
What Is Long Division?
Long division is a systematic, multi-step algorithm for dividing larger numbers that can't be solved easily through mental math or simple calculation. It breaks complex division into manageable steps—divide, multiply, subtract, bring down—repeated until you've used all digits from the number being divided.
We use long division instead of mental or short division when:
Numbers are too large to divide mentally
We need precise answers with remainders or decimals
We're working with multi-digit divisors
We need to show our work clearly for homework or tests
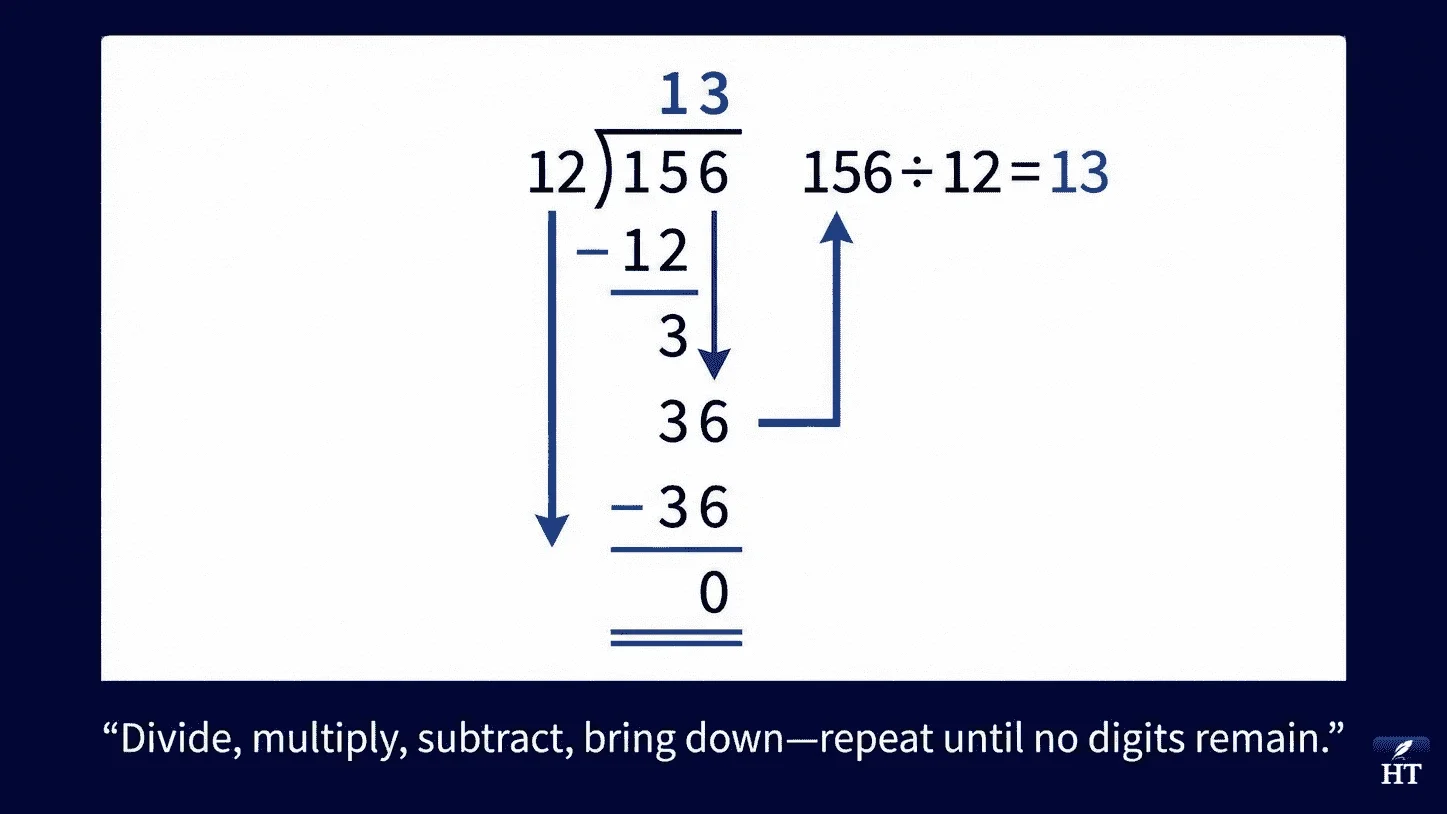
Simple conceptual example: If you need to divide 156 by 12, you can't immediately see the answer. Long division helps you work through it systematically: 12 goes into 15 once (write 1), multiply 1 × 12 = 12, subtract 15 - 12 = 3, bring down 6 to make 36, 12 goes into 36 three times (write 3), and you're done—the answer is 13.
Understanding how to do long division step by step builds a foundation for more advanced math, including algebra, polynomial division, and calculus.
When Do We Use Long Division in Real Life?
Long division appears in practical situations more often than you might think:
Splitting costs or bills – Dividing a restaurant check evenly among friends
Distributing items equally – Sharing 156 candies among 12 students
Calculating rates and averages – Finding price per unit or average speed over distance
Measuring and converting units – Determining how many feet in a certain number of inches
Solving word problems – Most story problems in school involve division scenarios
Budgeting and financial planning – Calculating monthly payments or savings goals
How to Do Long Division (Step-by-Step)
Learning how to do long division becomes straightforward when you follow a consistent pattern. The process uses the same sequence regardless of problem size: divide → multiply → subtract → bring down, repeated until complete.
Let's walk through the universal method using a clear example: 156 ÷ 12
Step 1 — Set Up the Long Division Problem
Write the problem using the long division symbol (also called the division bracket or "bus stop" in some regions):
___
12 ) 156
Key terms:
Dividend (156) – The number being divided, written under/inside the bracket
Divisor (12) – The number you're dividing by, written outside/to the left
Quotient – The answer, written on top of the bracket
Proper setup ensures all your work stays organized and readable.
Step 2 — Divide
Ask yourself: "How many times does the divisor go into the first digit(s) of the dividend?"
Look at the first digit of 156, which is 1. Can 12 go into 1? No—12 is larger than 1.
So look at the first TWO digits: 15. How many times does 12 go into 15? Once (because 12 × 1 = 12, but 12 × 2 = 24, which is too large).
Write 1 above the 5 in your quotient:
1__
12 ) 156
Step 3 — Multiply
Multiply the divisor by the quotient digit you just wrote: 12 × 1 = 12
Write this result below the digits you used (15):
1__
12 ) 156
12
Step 4 — Subtract
Subtract the number you just wrote from the portion of the dividend above it:
15 - 12 = 3
1__
12 ) 156
-12
___
3
Step 5 — Bring Down
Bring down the next digit from the dividend (the 6) next to your remainder:
1__
12 ) 156
-12
___
36
Step 6 — Repeat Until There Are No Digits Left
Now repeat the cycle with 36:
Divide: How many times does 12 go into 36? 3 times (12 × 3 = 36) Write 3 in the quotient above the 6
13
12 ) 156
-12
___
36
Multiply: 12 × 3 = 36 Subtract: 36 - 36 = 0
13
12 ) 156
-12
___
36
-36
___
0
No more digits to bring down, and the remainder is 0, so you're finished.
Final answer: 156 ÷ 12 = 13
The key to mastering long division is recognizing this pattern: divide–multiply–subtract–bring down, repeated in a cycle until you've processed all digits.
Long Division Examples With Whole Numbers
Let's work through examples of how to do long division with increasing complexity to build your confidence.
Example 1: 2-Digit ÷ 1-Digit (84 ÷ 7)
This is a beginner-friendly problem:
12
7 ) 84
-7
___
14
-14
___
0
Steps:
7 goes into 8 once → write 1
Multiply: 1 × 7 = 7
Subtract: 8 - 7 = 1
Bring down 4 → make 14
7 goes into 14 twice → write 2
Multiply: 2 × 7 = 14
Subtract: 14 - 14 = 0
Answer: 84 ÷ 7 = 12
Example 2: 3-Digit ÷ 1-Digit (225 ÷ 5)
Adding one more digit:
45
5 ) 225
-20
___
25
-25
___
0
Steps:
5 goes into 22 four times → write 4
Multiply: 4 × 5 = 20
Subtract: 22 - 20 = 2
Bring down 5 → make 25
5 goes into 25 five times → write 5
Multiply: 5 × 5 = 25
Subtract: 25 - 25 = 0
Answer: 225 ÷ 5 = 45
Example 3: 3-Digit ÷ 2-Digit (368 ÷ 16)
This introduces estimation for choosing quotient digits:
23
16 ) 368
-32
___
48
-48
___
0
Steps:
16 goes into 36 twice (estimate: 16 × 2 = 32) → write 2
Multiply: 2 × 16 = 32
Subtract: 36 - 32 = 4
Bring down 8 → make 48
16 goes into 48 three times → write 3
Multiply: 3 × 16 = 48
Subtract: 48 - 48 = 0
Answer: 368 ÷ 16 = 23
Example 4: Long Division With Big Numbers (12,648 ÷ 24)
Understanding how to do long division with big numbers is easier than it looks—the steps remain identical, just longer:
527
24 ) 12,648
-120
____
64
-48
____
168
-168
____
0
Steps summary:
24 into 126 goes 5 times (5 × 24 = 120)
Subtract: 126 - 120 = 6
Bring down 4 → make 64
24 into 64 goes 2 times (2 × 24 = 48)
Subtract: 64 - 48 = 16
Bring down 8 → make 168
24 into 168 goes 7 times exactly (7 × 24 = 168)
Subtract: 168 - 168 = 0
Answer: 12,648 ÷ 24 = 527
The process doesn't change for larger numbers—you simply repeat the cycle more times.
How to Do Long Division with Remainders
Many students wonder how to do long division with remainders when problems don't divide evenly. A remainder is what's left over after dividing as far as possible with whole numbers.
Example: 47 ÷ 6
7
6 ) 47
-42
___
5
Steps:
6 goes into 47 seven times (6 × 7 = 42)
Subtract: 47 - 42 = 5
No more digits to bring down
The 5 is your remainder
How to write answers with remainders:
Method 1 — Using "R" notation: 47 ÷ 6 = 7 R5 (read as "7 remainder 5")
Method 2 — As a mixed number: 47 ÷ 6 = 7 5/6 (the remainder becomes the numerator over the divisor)
Both formats are correct—use whichever your teacher or assignment requires.
Another example: 100 ÷ 9
9 × 11 = 99
100 - 99 = 1
Answer: 11 R1 or 11 1/9
Understanding how to do long division with a remainder prepares you for more complex problems and real-world situations where things don't divide evenly.
How to Do Long Division with Decimals
Learning how to do long division with decimals involves two main scenarios, each with specific techniques.
Case 1: Decimal in the Dividend Only
When only the number being divided has a decimal, align the decimal point in your quotient directly above the decimal in the dividend.
Example: 12.6 ÷ 3
4.2
3 ) 12.6
-12
____
0.6
-0.6
____
0
Steps:
Place decimal point in quotient above the decimal in 12.6
3 into 12 goes 4 times → write 4
Multiply: 4 × 3 = 12
Subtract: 12 - 12 = 0
Bring down 6 (after decimal)
3 into 6 goes 2 times → write 2 (after decimal in quotient)
Multiply: 2 × 3 = 6
Subtract: 6 - 6 = 0
Answer: 12.6 ÷ 3 = 4.2
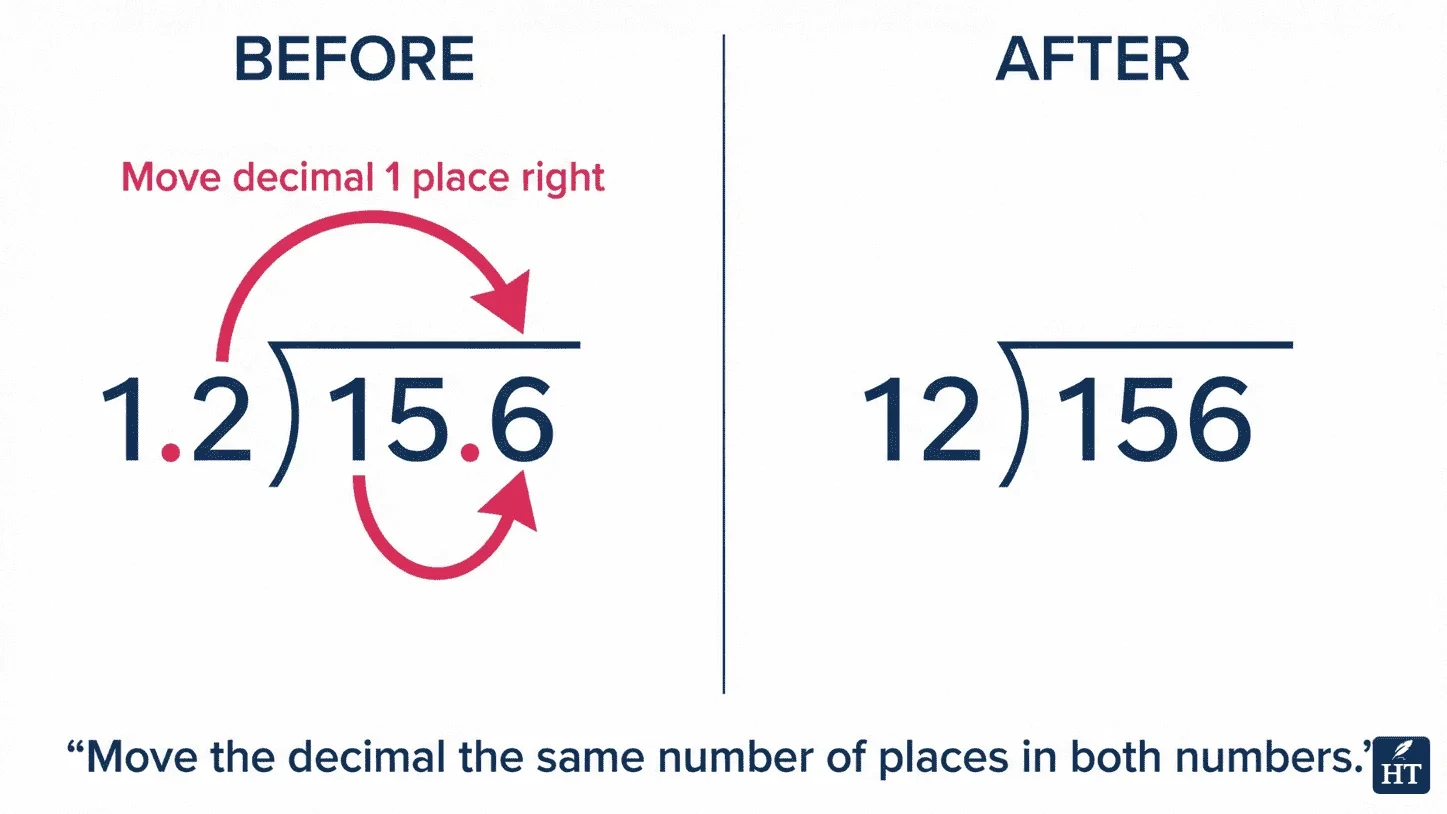
Case 2: Decimal in the Divisor
When the divisor has a decimal, you must move the decimal point to make it a whole number, then move the decimal in the dividend the same number of places.
Example: 15.6 ÷ 1.2
Step 1: Move decimal one place right in both numbers:
1.2 becomes 12
15.6 becomes 156
Step 2: Now solve 156 ÷ 12:
13
12 ) 156
-12
___
36
-36
___
0
Answer: 15.6 ÷ 1.2 = 13
Money application example: If 12.5 pounds of apples cost $25.00, what's the price per pound?
$25.00 ÷ 12.5 → Move decimal one place: 250 ÷ 125 = 2
Answer: $2.00 per pound
How to Do Long Division With 2-, 3-, 4-, and 6-Digit Numbers
Students often search for how to do long division with 2 digits, how to do long division with 3 digits, how to do long division with 4 digits, or even how to do long division with 6 digits. The important principle is: the process never changes, only the length increases.
| Dividend Size | Example Problem | Key Point |
|---|---|---|
| 2-digit | 48 ÷ 6 = 8 | Simplest form, often one cycle |
| 3-digit | 156 ÷ 12 = 13 | Standard classroom problems |
| 4-digit | 2,436 ÷ 14 = 174 | More cycles, same pattern |
| 6-digit | 123,456 ÷ 24 = 5,144 | Many cycles, requires patience |
Working with longer numbers:
Write neatly and keep columns aligned
Take your time with each cycle
Check your subtraction at each step
Don't rush—accuracy matters more than speed
Example structure for 4-digit ÷ 2-digit (1,848 ÷ 21):
The answer is 88, found by:
21 into 184 goes 8 times
Bring down 8 → make 168
21 into 168 goes 8 times
Result: 88
Whether you're dividing how to do long division with three digits or six, follow divide–multiply–subtract–bring down consistently.
How to Do Long Division for 4th Graders
Fourth graders typically encounter how to do long division for 4th graders as a major new skill. At this level, focus on building confidence with fundamentals.
4th grade long division focuses on:
1-digit divisors (dividing by numbers 2-9)
Whole number dividends (no decimals yet)
Simple remainders (understanding what's left over)
2-digit and 3-digit dividends (manageable size)
Teaching tips for 4th grade success:
Use place value language: "How many groups of 6 fit into 48?"
Draw visual aids: Arrays, base-ten blocks, or groups of objects help conceptualize division
Practice multiplication facts: Strong times tables make division estimates easier
Write neatly: Messy work leads to errors—keep columns straight
Check answers by multiplying: Multiply quotient × divisor to verify
Common 4th Grade Long Division Problem Types
Basic division: 84 ÷ 7, 96 ÷ 8, 72 ÷ 6
With small remainders: 50 ÷ 7 (7 R1), 38 ÷ 5 (7 R3)
2-digit ÷ 1-digit: 48 ÷ 4, 63 ÷ 3, 91 ÷ 7
3-digit ÷ 1-digit: 144 ÷ 6, 225 ÷ 5, 168 ÷ 8
Word problems: "If 156 cookies are shared equally among 12 students, how many does each student get?"
Start with problems that divide evenly, then gradually introduce remainders once the basic pattern feels comfortable.
How to Do Long Division for 5th Graders
By fifth grade, students advance to how to do long division for 5th graders with increased complexity and real-world applications.
5th grade long division introduces:
2-digit divisors (dividing by numbers like 12, 15, 24)
Simple decimals (answers with tenths and hundredths)
Larger dividends (4-digit and 5-digit numbers)
Word problems with multiple steps
Key skills for 5th grade:
Estimation: Guess quotient digits by rounding divisors
Decimal placement: Aligning decimal points correctly
Multi-step problems: Division combined with other operations
Checking work: Using multiplication to verify answers
Bridging From 4th Grade to 5th Grade Skills
Complexity increases in these ways:
More digits: Moving from 156 ÷ 6 (4th grade) to 1,248 ÷ 16 (5th grade)
Decimals appear: Understanding 25.2 ÷ 6 = 4.2
Estimation becomes essential: 2-digit divisors require educated guessing
Mixed operations: "First find the total, then divide by the number of groups"
Real-world contexts: Distance problems, rate problems, unit conversions
Practice problems at the 5th-grade level should mix whole numbers, remainders, and simple decimals to build versatility.
How to Do Long Division with Fractions
Understanding how to do long division with fractions connects two important concepts: division and fractional notation.
Key connections:
Division creates fractions: When you divide 3 by 4 and can't get a whole number answer, the result is the fraction 3/4. Long division and fractions are two ways of expressing the same relationship.
Dividing by a fraction: To divide by a fraction, use the "keep-change-flip" method (multiply by the reciprocal):
Example: 6 ÷ 1/2
Keep the 6
Change division to multiplication
Flip 1/2 to 2/1
Calculate: 6 × 2 = 12
Expressing remainders as fractions: When long division produces a remainder, you can write it as a fraction:
Example: 17 ÷ 5
5 goes into 17 three times (3 × 5 = 15)
Remainder: 17 - 15 = 2
Answer: 3 R2 or 3 2/5
Converting division to fractions:
7 ÷ 8 = 7/8
15 ÷ 4 = 15/4 = 3 3/4
22 ÷ 7 = 22/7 ≈ 3.14 (or 3 R1)
This conceptual link helps students understand that division, fractions, and decimals all represent ways of expressing parts of wholes.
How to Do Long Division with Variables and Polynomials
Advanced students need to know how to do long division with variables and how to do long division with polynomials. The same divide–multiply–subtract–bring down pattern applies, but with algebraic terms instead of digits.
Polynomial Long Division Step-by-Step
Example: Divide (x² + 7x + 12) by (x + 3)
Set up like regular long division:
x + 4
___________
x + 3 ) x² + 7x + 12
x² + 3x
________
4x + 12
4x + 12
_______
0
Steps:
1. Divide leading terms: x² ÷ x = x (write in quotient)
2. Multiply: x(x + 3) = x² + 3x (write below)
3. Subtract: (x² + 7x) - (x² + 3x) = 4x
4. Bring down: Bring down +12 → make 4x + 12
5. Divide again: 4x ÷ x = 4 (write in quotient)
6. Multiply: 4(x + 3) = 4x + 12
7. Subtract: (4x + 12) - (4x + 12) = 0
Answer: (x² + 7x + 12) ÷ (x + 3) = x + 4
Common Mistakes in Polynomial Long Division
Not aligning like terms – Keep x² terms above x² terms, x terms above x terms
Sign errors – Be careful when subtracting negative terms: minus a negative becomes addition
Skipping missing terms – If x² + 12 lacks an x term, write it as x² + 0x + 12 to maintain alignment
Forgetting to bring down – Each term must be brought into the working area
Stopping too early – Continue until the remainder has a lower degree than the divisor
Polynomial division follows the exact same pattern as numerical long division—recognizing this connection makes algebra much less intimidating.
How to Do Long Division Using the Square Root Long Division Method
Some students search for how to do long division square root, which refers to an advanced technique for finding square roots manually before calculators.
The square root long division method:
This algorithm finds square roots digit-by-digit using a pattern similar to long division. It's rarely taught in modern classrooms but appears in competition math and historical mathematics.
High-level steps for √256:
Group digits in pairs from right: 2|56
Find largest number whose square ≤ first group: 1² = 1 (too small), 2² = 4 (too large), so use 1
Write 1 above, subtract 1 from 2, bring down 56
Double the quotient (2), find next digit
Continue pattern to get 16
Example: √144 = 12
1|44
1² = 1, subtract, bring down 44
Try 2: (20 + 2) × 2 = 44 ✓
Answer: 12
Note: This is an enrichment skill, not necessary for basic long division. Most students use calculators for square roots today, but understanding the algorithm deepens number sense.
Common Long Division Mistakes and How to Fix Them
Recognizing frequent errors helps you avoid them:
Mistake: Misplacing digits in the quotient
Problem: Writing digits in the wrong position above the dividend
Fix: Align each quotient digit directly above the last digit you used in that division step
Mistake: Forgetting to bring down a digit
Problem: Skipping the "bring down" step and getting stuck
Fix: After every subtraction, check if there are more digits to bring down; mark them off as you go
Mistake: Stopping before using all digits
Problem: Ending the problem when there's still a remainder with digits left
Fix: Continue divide–multiply–subtract–bring down until you've brought down every digit from the dividend
Mistake: Misunderstanding remainders
Problem: Not knowing what to do when the last subtraction leaves a number
Fix: Recognize this as a remainder; express as "R#" or as a fraction (remainder/divisor)
Mistake: Misaligning decimals
Problem: Placing the decimal point incorrectly in the quotient
Fix: Always align the decimal in your answer directly above the decimal in the dividend
Mistake: Choosing the wrong quotient digit
Problem: Guessing a digit that's too large or too small
Fix: Estimate carefully; if your multiplication result is larger than the working number, try a smaller digit
Mistake: Subtraction errors
Problem: Making arithmetic mistakes during the subtract step
Fix: Double-check each subtraction; if your remainder seems too large, recheck your math
Long Division Practice Problems
Test your skills with these problems covering different difficulty levels:
Basic Whole Numbers:
96 ÷ 8 = ?
144 ÷ 12 = ?
252 ÷ 9 = ?
With Remainders: 4. 75 ÷ 7 = ? 5. 100 ÷ 9 = ?
With Decimals: 6. 18.6 ÷ 3 = ? 7. 24.5 ÷ 0.5 = ?
Big Numbers: 8. 1,848 ÷ 21 = ?
Polynomial (Bonus): 9. (x² + 5x + 6) ÷ (x + 2) = ?
Answer Key
96 ÷ 8 = 12
144 ÷ 12 = 12
252 ÷ 9 = 28
75 ÷ 7 = 10 R5 or 10 5/7
100 ÷ 9 = 11 R1 or 11 1/9
18.6 ÷ 3 = 6.2
24.5 ÷ 0.5 = 49 (move decimals: 245 ÷ 5)
1,848 ÷ 21 = 88
(x² + 5x + 6) ÷ (x + 2) = x + 3
Practice these problems until the pattern feels automatic, then create your own to build mastery.
Conclusion
Learning how to do long division transforms from an intimidating challenge into a manageable skill once you understand the repeating pattern: divide → multiply → subtract → bring down. Start with simple whole-number problems to build confidence, then progressively add remainders, decimals, bigger numbers, and eventually variables and polynomials as your comfort grows.
Remember that mistakes are part of learning—even experienced mathematicians occasionally misalign digits or make subtraction errors. The key is working systematically, checking each step, and practicing regularly. Whether you're a 4th grader encountering long division for the first time, a 5th grader tackling 2-digit divisors, or a high school student working with polynomials, the fundamental process remains the same.
With the step-by-step methods, worked examples, and practice problems in this guide, you now have the tools to master how to do long division confidently. Keep practicing, stay patient with yourself, and celebrate your progress.
Ready to strengthen more math skills? Visit HYE Tutors for comprehensive guides on multiplication strategies, fraction operations, decimal division, and polynomial algebra designed to build your mathematical confidence.
References:
Khan Academy: Long Division – Comprehensive video lessons and practice
Math is Fun: Long Division – Interactive examples with animations
IXL Math: Division Practice – Grade-specific practice problems