What Are the Factors in Math? Everything You Need to Know
If you've ever wondered what are factors in math, you're tackling a fundamental concept that appears throughout arithmetic, algebra, and problem-solving. Students often confuse factors with multiples, struggle to identify all factors of a number, or don't understand how factors connect to division, products, and algebraic expressions. Simply put, factors are the building blocks of multiplication—the numbers that combine to create other numbers.
This comprehensive guide will explain what factors mean in mathematical terms, show you how to find them systematically, introduce factor pairs and factor trees, clarify the difference between factors and related concepts like multiples and products, and demonstrate how factors work in algebra. Whether you're learning basic multiplication or factoring algebraic expressions, understanding factors builds your mathematical foundation.
Let's explore this essential concept with clear examples and practical applications
“In math, factors are numbers that multiply together to give another number. A factor divides a number exactly, with no remainder. For example, 1, 2, and 4 are factors of 4 because each divides evenly into 4. Factors are used in multiplication, division, algebra expressions, and problem-solving across many areas of math.”
What Are Factors in Math?
Factors in math are whole numbers that divide evenly into another number with no remainder. When you multiply two factors together, they produce a specific number called the product. Every factor of a number divides into that number perfectly—meaning the division results in a whole number, not a decimal or fraction.
Formal definition: A number a is a factor of number b if b ÷ a results in a whole number with no remainder.
Simple examples:
Factors of 4: 1, 2, 4
4 ÷ 1 = 4 ✓
4 ÷ 2 = 2 ✓
4 ÷ 4 = 1 ✓
Factors of 6: 1, 2, 3, 6
6 ÷ 1 = 6 ✓
6 ÷ 2 = 3 ✓
6 ÷ 3 = 2 ✓
6 ÷ 6 = 1 ✓
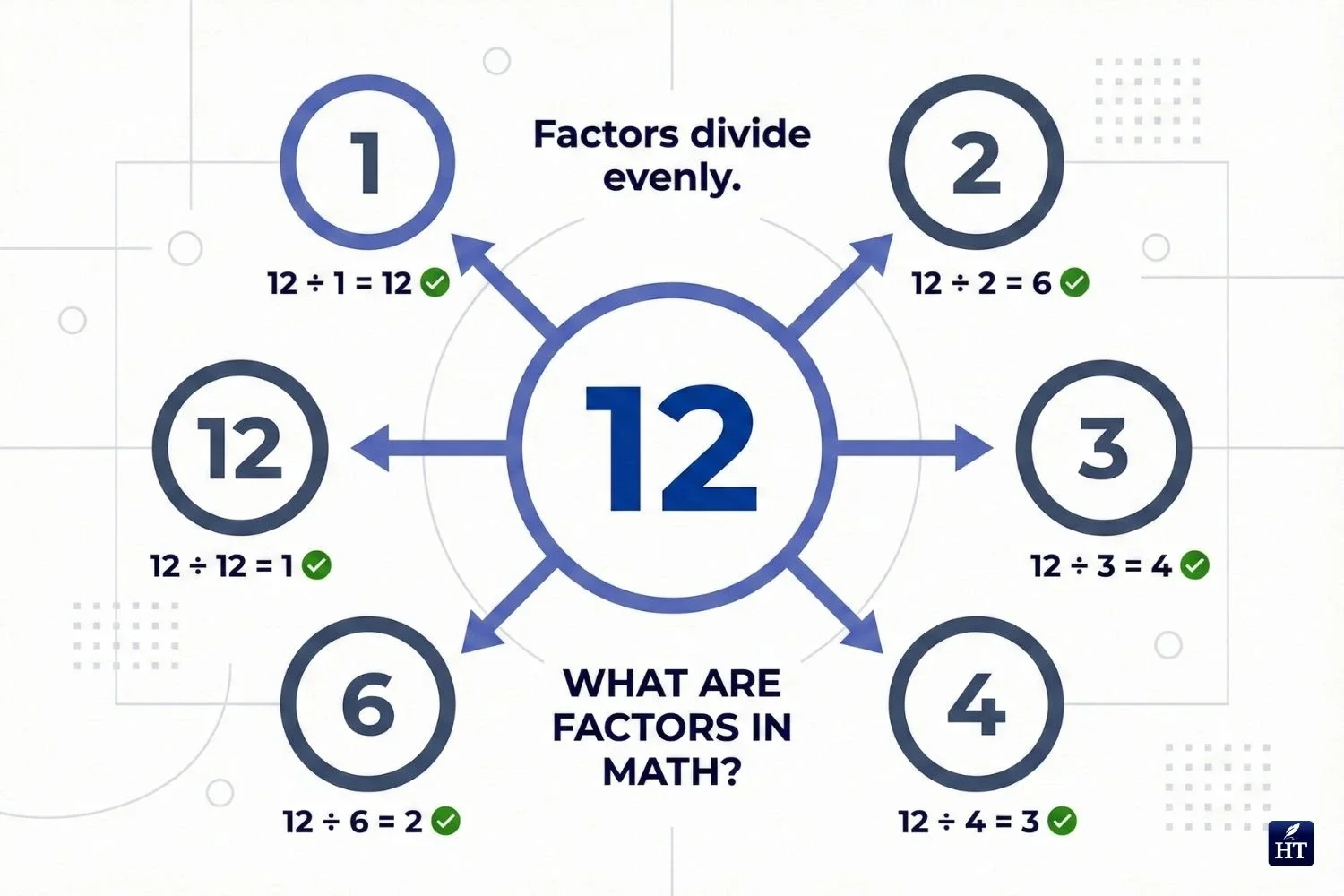
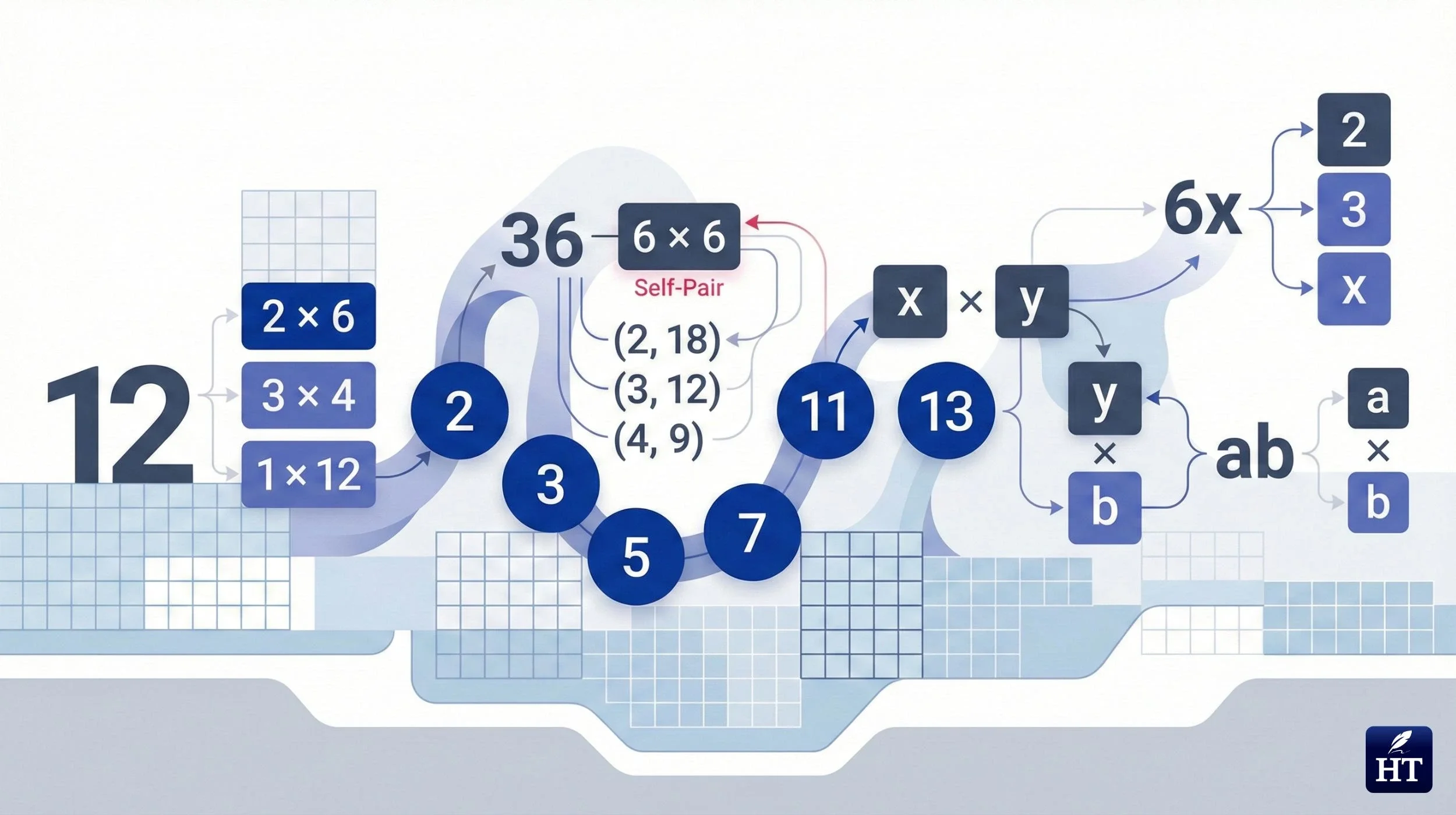
Factors of 12: 1, 2, 3, 4, 6, 12
All these numbers divide into 12 evenly
Understanding what are the factors in math and what are factors in math terms helps you work with multiplication, division, fractions, greatest common factors (GCF), and least common multiples (LCM).
Key insight: The number itself and 1 are always factors of any number. For instance, 12 has 1 and 12 as factors, along with the numbers in between that divide evenly.
Factors Explained in Simple Words
Think of factors as the numbers you can multiply together to make another number. If you can divide a number by another number and get a whole number answer with nothing left over, that's a factor.
Example: The factors of 8 are 1, 2, 4, and 8 because:
1 × 8 = 8
2 × 4 = 8
How to Find Factors of a Number
Finding all factors of a number systematically ensures you don't miss any. Follow this step-by-step method to identify every factor.
Step 1: Start With 1 and the Number Itself
Every whole number has at least two factors: 1 and itself.
Why?
Any number multiplied by 1 equals itself: 1 × 15 = 15
Any number divided by itself equals 1: 15 ÷ 15 = 1
So for 15, start your factor list with: 1, 15
Step 2: Test Numbers That Divide Evenly
Work through numbers from 2 upward, testing if each divides evenly into your target number.
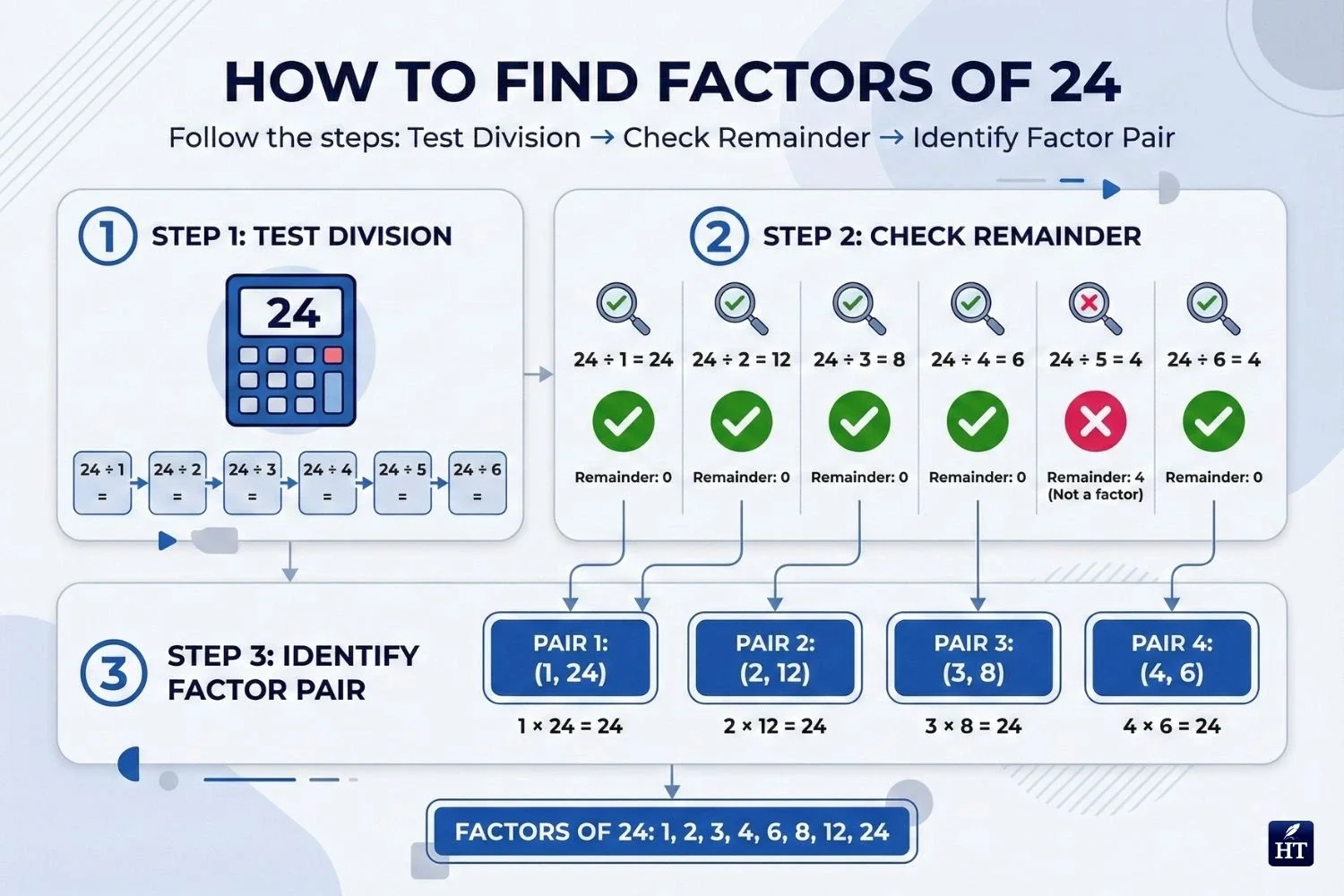
Finding factors of 24:
Test 2: Does 24 ÷ 2 work evenly? Yes → 24 ÷ 2 = 12 ✓ Test 3: Does 24 ÷ 3 work evenly? Yes → 24 ÷ 3 = 8 ✓ Test 4: Does 24 ÷ 4 work evenly? Yes → 24 ÷ 4 = 6 ✓ Test 5: Does 24 ÷ 5 work evenly? No → 24 ÷ 5 = 4.8 ✗ Test 6: Does 24 ÷ 6 work evenly? Yes → 24 ÷ 6 = 4 ✓
When to stop: You can stop testing when you reach the square root of the number. For 24, the square root is about 4.9, so once you've tested up to 5, you've found all factors. Any factors larger than the square root will have already appeared as results when testing smaller numbers.
Step 3: List All Factor Pairs
As you test each number, you're discovering factor pairs—two numbers that multiply together to give the original number.
Complete factor list for 24: 1, 2, 3, 4, 6, 8, 12, 24
Notice how factors come in pairs: (1, 24), (2, 12), (3, 8), (4, 6)
What Are Factor Pairs in Math?
Factor pairs in math are two numbers that multiply together to produce a specific number. Every factor belongs to at least one pair, and finding factor pairs helps you identify all factors systematically.
What are factor pairs in math? They're complementary factors that combine through multiplication to create the original number.
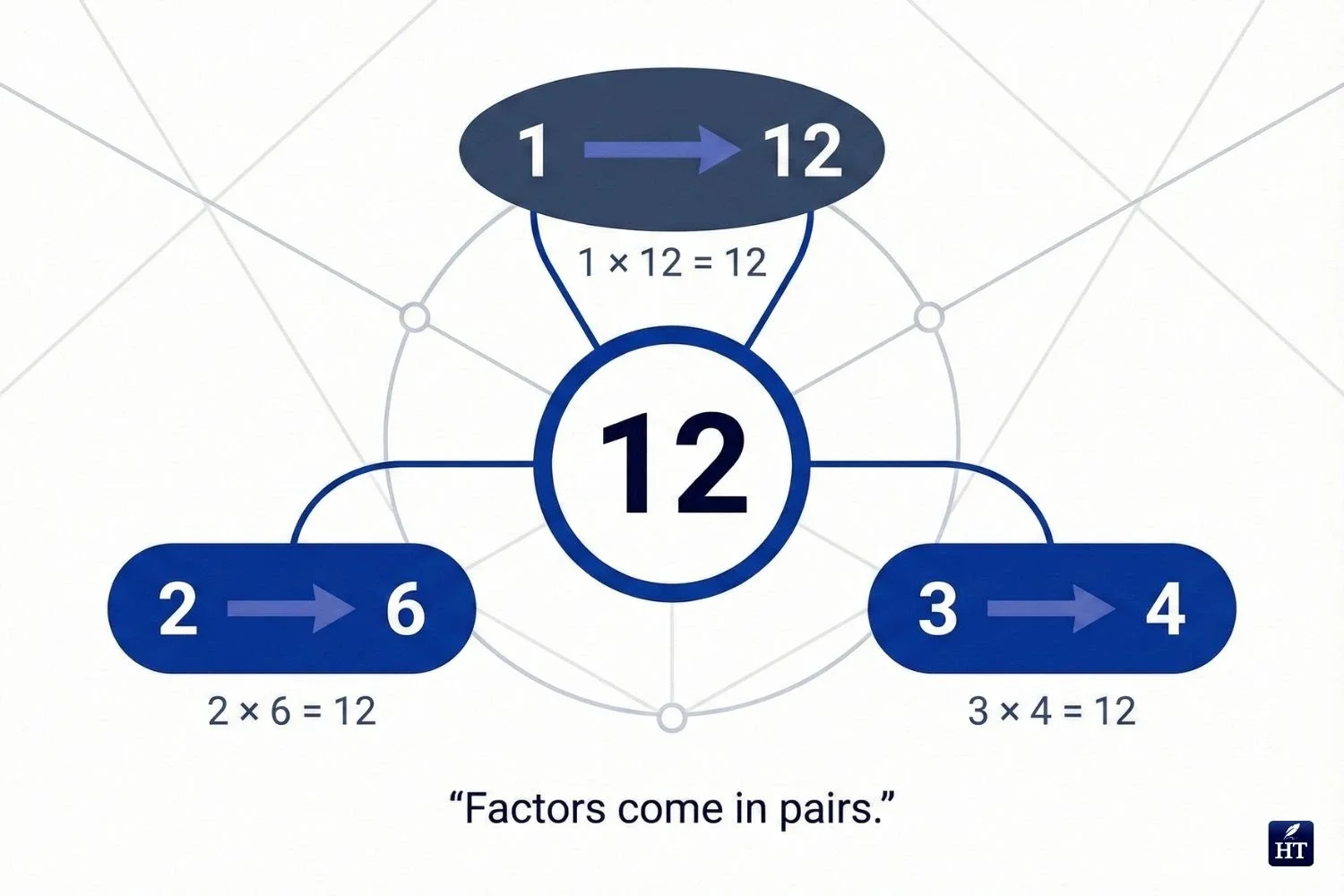
Factor pairs of 12:
1 × 12 = 12 → (1, 12)
2 × 6 = 12 → (2, 6)
3 × 4 = 12 → (3, 4)
Factor pairs of 20:
1 × 20 = 20 → (1, 20)
2 × 10 = 20 → (2, 10)
4 × 5 = 20 → (4, 5)
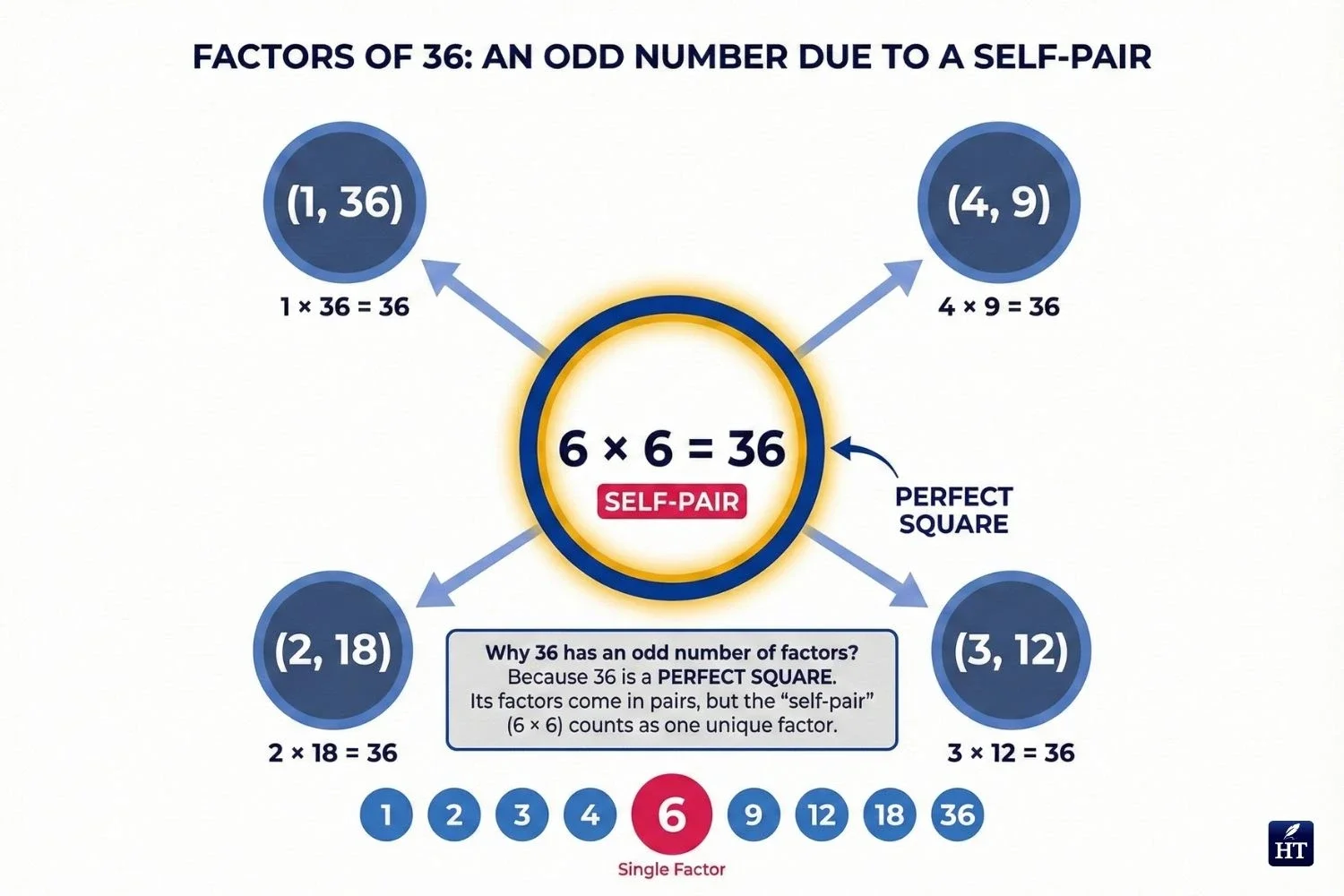
Factor pairs of 36:
(1, 36), (2, 18), (3, 12), (4, 9), (6, 6)
Notice that 36 has an odd number of total factors (9 factors) because 6 × 6 = 36—it pairs with itself. Numbers that are perfect squares always have an odd number of factors.
Positive Factor Pairs vs Negative Factor Pairs
For most basic math, we work only with positive factors. However, in algebra and higher mathematics, negative numbers can also be factors.
Positive factor pairs of 12: (1, 12), (2, 6), (3, 4)
Including negative factor pairs: (-1, -12), (-2, -6), (-3, -4)
Both positive and negative pairs multiply to give positive 12 because negative × negative = positive. In typical elementary and middle school math, "factors" refers only to positive whole numbers unless otherwise specified.
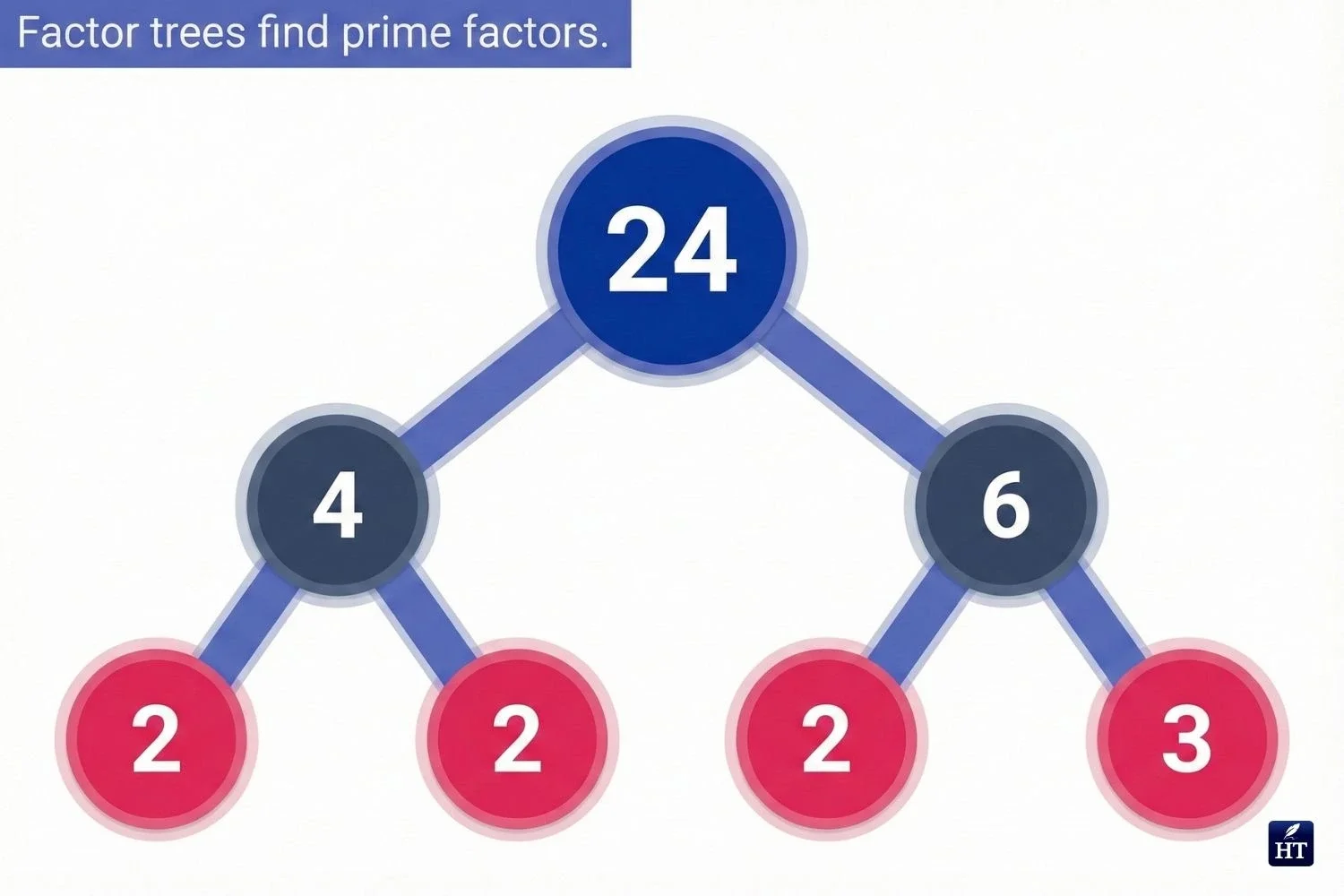
What Is a Factor Tree in Math?
A factor tree in math is a visual diagram that breaks down a number into its prime factors through repeated division. Understanding what are factor trees in math helps you find the prime factorization of any composite number.
How factor trees work: Start with your number, divide it by any factor, then continue dividing the results until you reach only prime numbers (numbers with exactly two factors: 1 and themselves).
Example: Factor tree for 24
24
/ \
2 12
/ \
2 6
/ \
2 3
Steps:
Start with 24
Divide by 2: 24 = 2 × 12
Divide 12 by 2: 12 = 2 × 6
Divide 6 by 2: 6 = 2 × 3
Both 2 and 3 are prime—stop
Prime factorization of 24: 2 × 2 × 2 × 3 = 2³ × 3
Example: Factor tree for 30
30
/ \
5 6
/ \
2 3
Prime factorization of 30: 2 × 3 × 5
When to Use a Factor Tree
Factor trees are particularly useful for:
Finding prime factorization – Breaking numbers into their prime building blocks
Calculating GCF (Greatest Common Factor) – Comparing prime factors of two or more numbers
Calculating LCM (Least Common Multiple) – Finding the smallest number that shares factors
Simplifying fractions – Identifying common factors in numerators and denominators
Understanding number structure – Seeing how composite numbers are built from primes
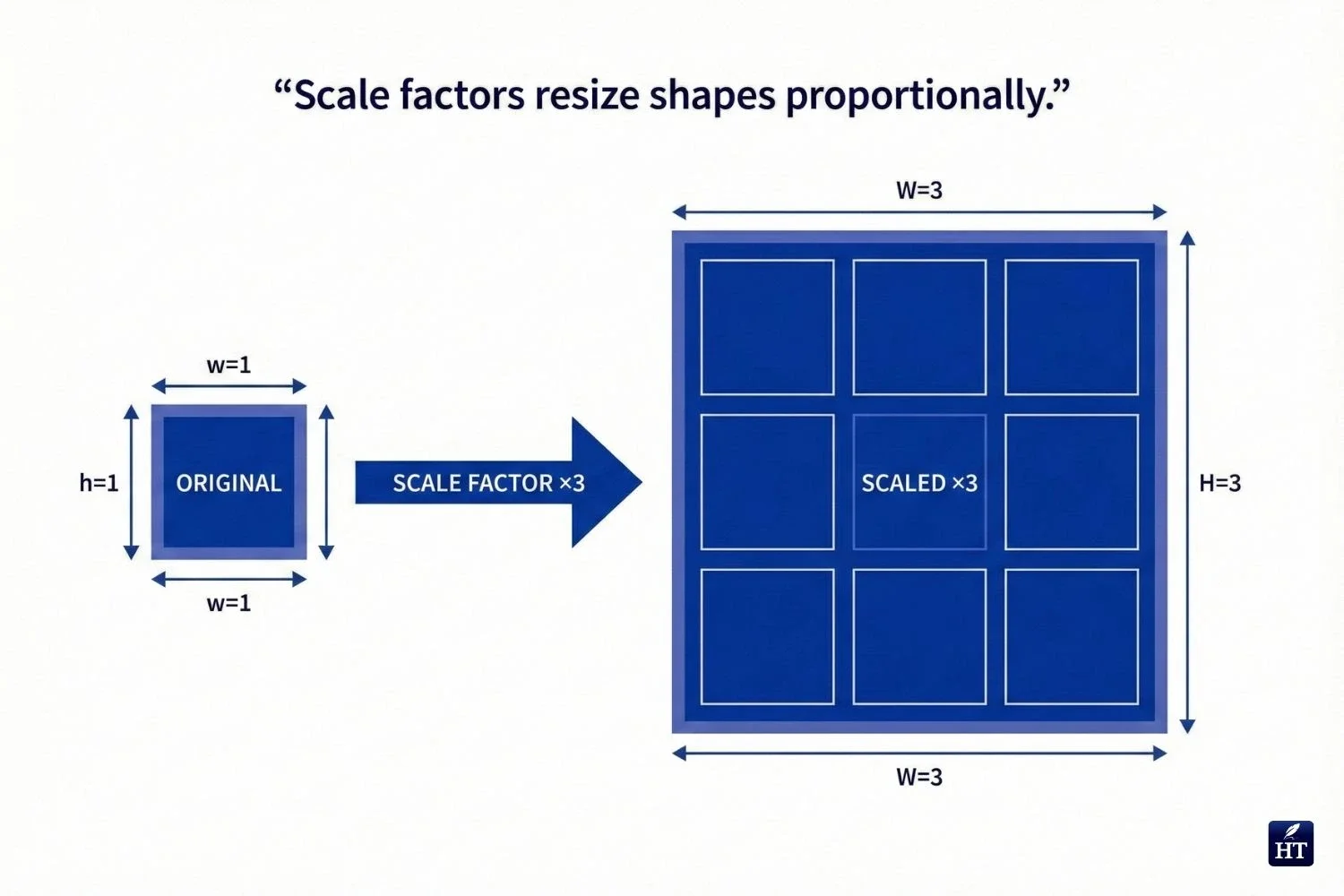
What Are Scale Factors in Math?
Scale factors in math are different from number factors—they're multipliers used to resize shapes, drawings, or measurements proportionally. A scale factor tells you how many times larger or smaller a new figure is compared to the original.
Definition: A scale factor is the ratio between corresponding measurements of two similar figures.
Formula: Scale Factor = New Size ÷ Original Size
Example in geometry: If a rectangle is 4 cm by 6 cm, and you apply a scale factor of 3:
New dimensions: (4 × 3) by (6 × 3) = 12 cm by 18 cm
The new rectangle is 3 times larger in each dimension
Scale factor less than 1: A scale factor of 0.5 (or 1/2) makes shapes smaller:
Original: 10 cm by 8 cm
Scale factor: 0.5
New size: 5 cm by 4 cm
Real-Life Examples of Scale Factors
Maps – A scale of 1:100 means 1 cm on the map represents 100 cm in reality (scale factor of 1/100)
Architectural drawings – Floor plans use scale factors like 1:50 to fit large buildings on paper
Model buildings and toys – A 1:24 scale model car is 24 times smaller than the real car
Enlarging photos or images – Doubling an image size uses a scale factor of 2
Reducing or enlarging recipes – Halving a recipe uses a scale factor of 0.5
Scale factors maintain proportions—all dimensions change by the same multiplier, keeping the shape similar to the original.
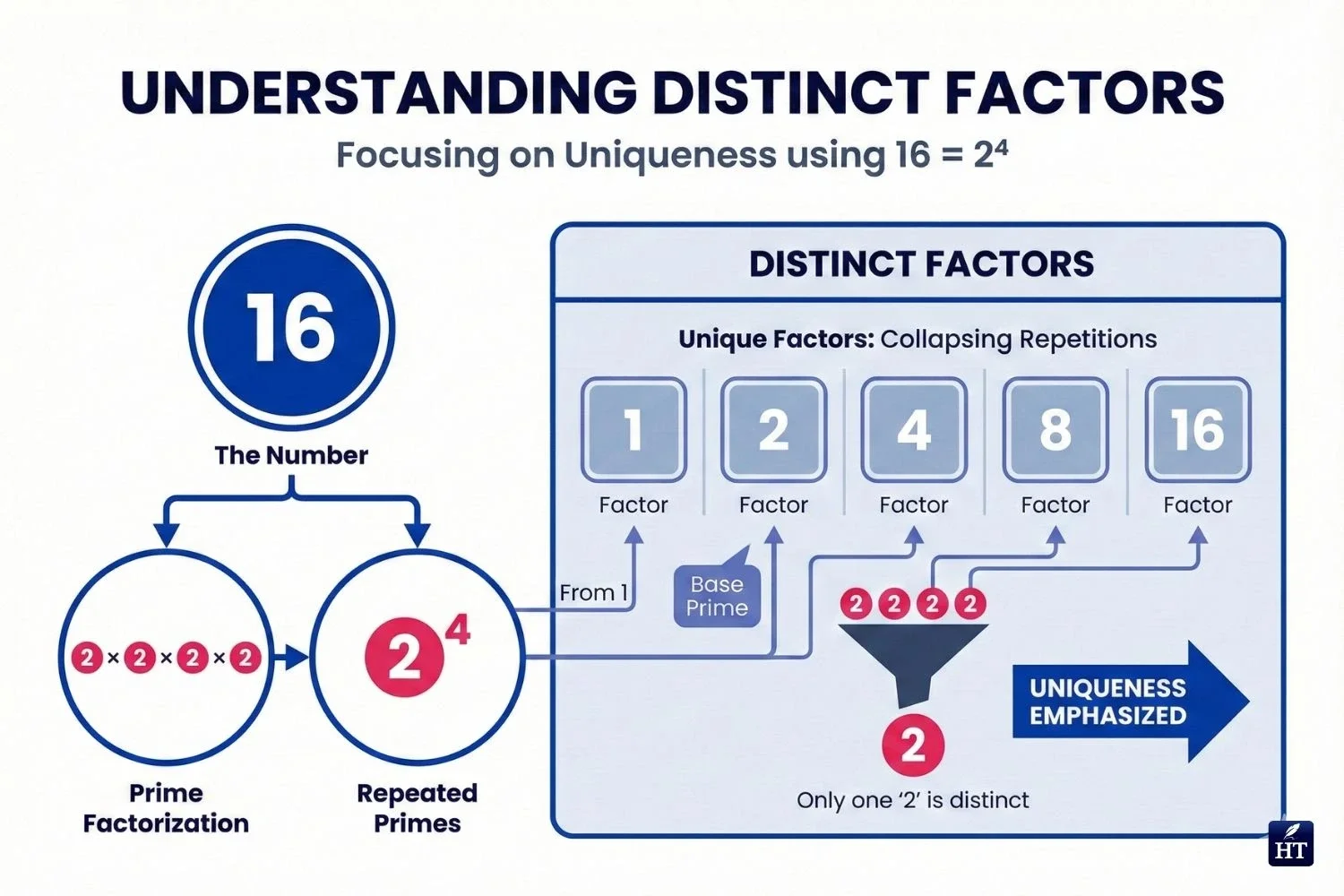
What Are Distinct Factors in Math?
Distinct factors in math are unique factors counted only once, even if they appear multiple times in the prime factorization of a number.
Example: Number 16
Prime factorization: 16 = 2 × 2 × 2 × 2 = 2⁴
All factors of 16: 1, 2, 4, 8, 16
Distinct factors: 1, 2, 4, 8, 16 (five distinct factors)
Even though 2 appears four times in the prime factorization, we only count it once as a distinct factor.
Example: Number 36
Prime factorization: 36 = 2 × 2 × 3 × 3 = 2² × 3²
All factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Distinct prime factors: 2 and 3 (only two distinct primes)
All distinct factors: 1, 2, 3, 4, 6, 9, 12, 18, 36 (nine distinct factors total)
The concept of distinct factors matters when counting factors, finding GCF, or working with sets in number theory.
Factors, Multiples, and Products — What's the Difference?
Students often confuse what are factors and multiples in math or wonder about what are factors and products in math. These related concepts have distinct meanings:
| Term | Definition | Relationship | Example (using 12) |
|---|---|---|---|
| Factors | Numbers that divide evenly into another number | Factors multiply to create the number | 1, 2, 3, 4, 6, 12 are factors of 12 |
| Multiples | Numbers created by multiplying by whole numbers | The number multiplied by 1, 2, 3, etc. | 12, 24, 36, 48... are multiples of 12 |
| Product | The result of multiplying numbers together | The answer to a multiplication problem | 3 × 4 = 12 (12 is the product) |
Key differences:
Factors divide INTO a number:
3 is a factor of 12 because 12 ÷ 3 = 4
Multiples are created BY multiplying a number:
24 is a multiple of 12 because 12 × 2 = 24
Products are the RESULT of multiplication:
When you multiply 6 × 2, the product is 12
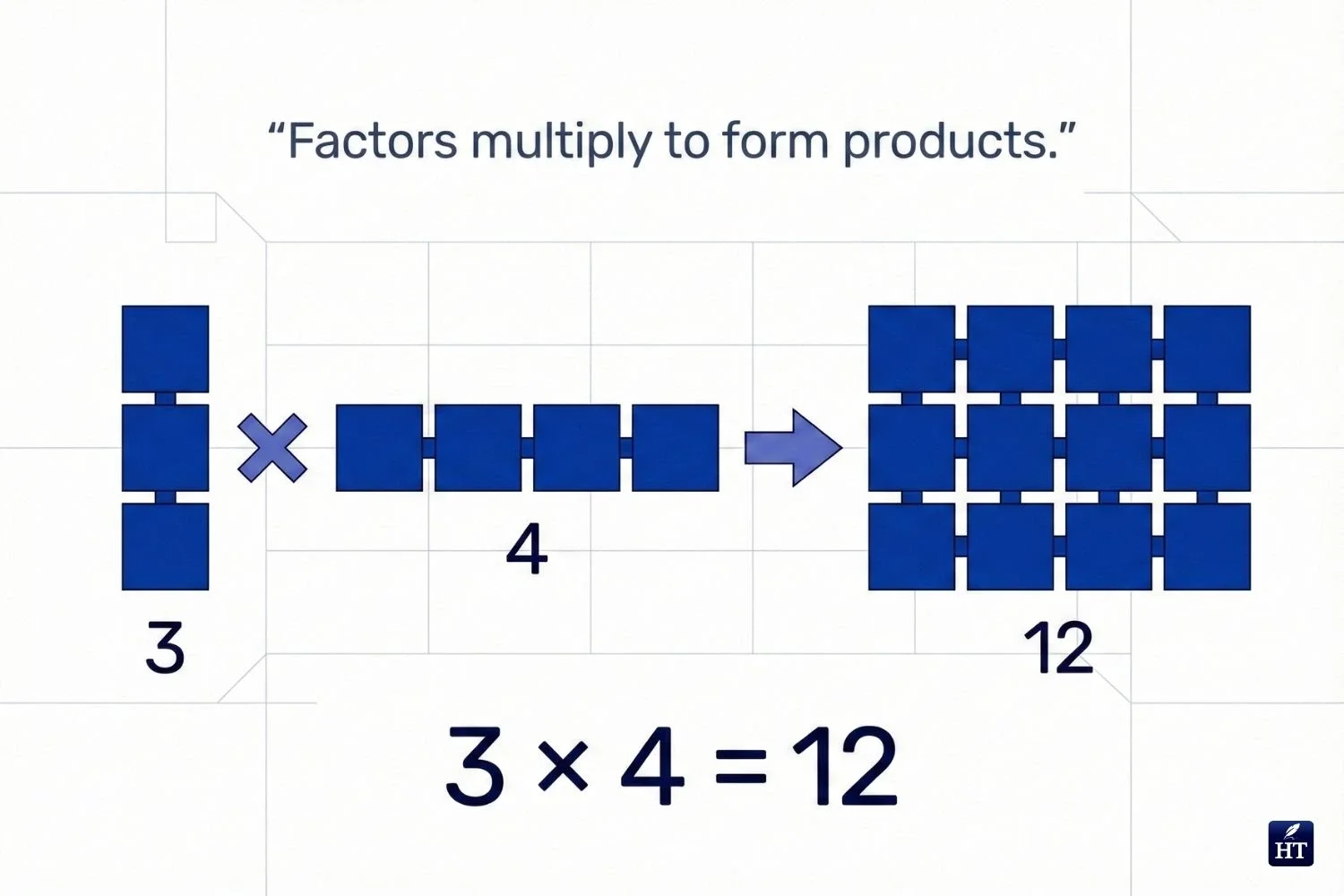
Simple Comparison Example
Using the equation: 3 × 4 = 12
Factors: 3 and 4 are factors of 12
Product: 12 is the product of 3 and 4
Multiples: 12 is a multiple of both 3 and 4
Another way to think about it:
Factors are smaller (or equal) → they divide into the number
Multiples are larger (or equal) → the number divides into them
Products are results → they're what you get from multiplication
Factors in Algebra and Math Expressions
Understanding what are factors in math algebra and what are factors in math expressions extends the concept beyond simple numbers to include variables and algebraic terms.
Factoring in algebra means finding numbers or expressions that multiply together to create an algebraic expression.
Numerical coefficients as factors:
Expression: 6x
Factors: 6 and x
Also: 2, 3, and x (since 2 × 3 × x = 6x)
Also: 1, 2, 3, 6, x, 2x, 3x, 6x
Expression: 12x²
Factors include: 1, 2, 3, 4, 6, 12, x, x², and various combinations
Factoring algebraic expressions:
Expression: x² + 5x
Common factor: x
Factored form: x(x + 5)
Expression: 2x + 8
Common factor: 2
Factored form: 2(x + 4)
Expression: 3x² + 6x
Common factor: 3x
Factored form: 3x(x + 2)
Why Factoring Matters in Algebra
Factoring algebraic expressions is essential for:
Simplifying expressions – Making complex expressions easier to work with
Solving equations – Many equations are solved by factoring, then using the zero product property
Finding common denominators – Adding and subtracting fractions with variables
Graphing functions – Factored forms reveal x-intercepts and behavior
Advanced mathematics – Factoring is foundational for calculus and higher math
Example: Solving by factoring
x² + 5x + 6 = 0 Factor: (x + 2)(x + 3) = 0 Solutions: x = -2 or x = -3
Understanding factors at the numerical level makes algebraic factoring much more intuitive.
Factors Examples (Quick Reference)
Here's a quick reference guide for commonly used numbers:
Factors of 6: 1, 2, 3, 6
Factor pairs: (1, 6), (2, 3)
Factors of 8: 1, 2, 4, 8
Factor pairs: (1, 8), (2, 4)
Factors of 10: 1, 2, 5, 10
Factor pairs: (1, 10), (2, 5)
Factors of 12: 1, 2, 3, 4, 6, 12
Factor pairs: (1, 12), (2, 6), (3, 4)
Factors of 15: 1, 3, 5, 15
Factor pairs: (1, 15), (3, 5)
Factors of 18: 1, 2, 3, 6, 9, 18
Factor pairs: (1, 18), (2, 9), (3, 6)
Factors of 20: 1, 2, 4, 5, 10, 20
Factor pairs: (1, 20), (2, 10), (4, 5)
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factor pairs: (1, 24), (2, 12), (3, 8), (4, 6)
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Factor pairs: (1, 30), (2, 15), (3, 10), (5, 6)
Conclusion
Understanding what are factors in math is fundamental to mastering multiplication, division, fractions, and algebra. Factors are simply the numbers that divide evenly into another number—the building blocks that multiply together to create products. Whether you're finding factor pairs, drawing factor trees for prime factorization, or factoring algebraic expressions, the core concept remains the same: factors divide into numbers with no remainder.
Practice identifying factors systematically, recognizing factor pairs, and distinguishing factors from related concepts like multiples and products. The more comfortable you become with factors at the basic level, the more naturally you'll understand their applications in GCF, LCM, fraction simplification, and algebraic factoring.
References:
Khan Academy: Factors and Multiples – Comprehensive lessons with practice problems
Math is Fun: Factors – Clear definitions and interactive examples
National Council of Teachers of Mathematics – Professional teaching standards and resources